본 내용은 아날로그 디바이스의 MT-004 “ The Good, the bad, and the Ugly Aspects of ADC Input Noise – Is No Noise good Noise?” 문서를 정리한 것이다.
1. 개요
ADC는 이상적으로는 “아날로그 입력 → 정확한 디지털 코드”를 만들어야 하지만, 현실의 ADC 내부 회로(샘플링 스위치, 비교기, 증폭기 등) 때문에 자체 잡음이 존재한다.
이 내부 잡음을 다음과 같이 모델링 할 수 있다. “잡음이 없는 이상적인 ADC 앞 단에, 입력과 직렬로 노이즈 전압원이 하나 있다”는 것이다. 이 노이즈 전압원이 input-referred noise이다. 즉, 실제로 입력에 노이즈가 있는 게 아니라 ADC 내부 잡음을 입력 쪽으로 환산한 값이다. Input-referred noise와 Quantization noise의 물리적 원인은 아예 다르다. Quantization noise는 ADC가 연속 값을 계단 값으로 양자화 하면서 생기는 오차임. 따라서 AC 신호가 있을 때만 통계적으로 “잡음처럼” 보임(이론 값 SNR =

dB). 하지만 Input-referred noise는 ADC 내부 아날로그 회로에서 발생DC 입력에서도 존재, ADC가 아무 신호를 받지 않아도 출력 코드가 흔들릴 수 있음.
보통은 input noise가 작을수록 SNR ↑, ENOB ↑ 이므로 성능이 향상된다. 하지만 반대로 noise를 이용하여 ADC의 성능을 개선할 수 있는 여지가 있다. 본 글에서는 평균과 dithering을 이용한 ADC 성능개선에 대해 정리한다.
2. INPUT-REFERRED NOISE (CODE TRANSITION NOISE)
이상적인 ADC의 전송 특성(transfer function)은 완벽한 계단(step)임. 입력 전압이 증가해도
어떤 임계값(threshold)에 도달하기 전 까지는 출력 코드가 절대 변하지 않아야 한다. 임계값에 도달하는 순간 출력 코드가 즉시 다음 코드로 점프한다. 이것을 Code transition noise = 0, Transition region width = 0이며, transition 포인트가 한 점이라고 한다.
실제 ADC에는 input-referred noise가 있다. 이 잡음 때문에 코드가 바뀌는 입력전압 지점이 한 점이 아니라 ‘구간’ 이 됨. 같은 입력 전압에서도 출력 코드가 왔다 갔다 할 수 있다. ADC의 입력 전압이 고정돼 있어도, Code transition noise에 의해 출력 코드가 두 코드 사이에서 랜덤하게 변동하게 된다. Transition region width는 이 잡음 때문에 생기는 불확실한 전압 구간이다. 코드 A일 수도, 코드 B일수도 있는 입력 전압 범위 임.
다음 그림에서 ACTUAL ADC Transition region width의 폭이 ≈ 1 LSB (p-p)인 경우이다. 입력 전압이 경계 전압 ±0.5 LSB 범위 안에 있으면, 출력 코드가 흔들린다.

이상적인 ADC에서는 코드 전이가 한 점에서 일어나지만, 실제 ADC에서는 input-referred noise 에 의해 코드 전이가 구간에서 일어나며, 이 폭을 code transition noise (transition region width)라 한다.
ADC 내부 잡음의 근본 원인은 저항 열잡음(Resistor noise), kT/C 잡음에 의한 것이다. 모든 저항은

형태의 열잡음을 발생하며, 샘플링 네트워크, 비교기 입력, 기준 회로 등에서 발생한다.
kT/C 잡음은 샘플링 커패시터에 전하를 저장할 때 발생하며, RMS 전압

이다. 특히 고속 / 고해상도 ADC의 주요 잡음임. 두 잡음은 항상 존재하며, DC 입력에서도 사라지지 않음
Code transition noise와 Input-referred noise는 같은 현상이며, 다만 Input-referred noise라는 용어가 주로 쓰임.
Input-referred noise의 영향은 ADC 입력에 DC전압을 넣고 출력되는 코드 값들의 히스토그램으로 확인한다.
AC 입력에서는 양자화 잡음, 왜곡, 클록 지터 등이 섞여서 순수한 내부 잡음을 보기 어렵다. 그래서 입력을 DC로 고정하고, ADC 내부 잡음만 관찰한다.
다음 그림은 Grounded-input histogram이다.

Grounded-input histogram을 얻는 방법은 다음과 같다. ADC 입력을 GND에 직접 연결하거나, 아주 안정적인 DC 전압원에 연결한다. 그리고 많은 출력 샘플을 수집하고, 각 코드가 몇 번 나왔는지 히스토그램으로 그린다.
특정 코드 주변에 종 모양 분포하므로 표준편차를 구할 수 있으며, 이것이 input rms noise이다. 단위는 LSB rms이다. ADC 사용자 입장에서 input- referred noise에 의한 분해능 영향을 LSB로 확인할 수 있다. 예를 들어 다음과 같이 판단할 수 있다. σ = 0.3 LSB rms → 매우 조용한 ADC, σ = 1 LSB rms → transition region이 꽤 넓음, σ > 1 LSB rms → DC 정확도 악화. 또한 input- referred noise 영향을 LSB가 아니라 전압 단위로 표현할 수 있다.

ADC의 Grounded input histogram을 통해, ADC의 성능과 문제 여부를 확인할 수 있다.
이상적인 ADC 출력 히스토그램은 DC 입력값을 중심으로 종 모양(정규분포) 형태가 된다. 내부 잡음이 여러 독립 원인(저항 잡음, kT/C 잡음, 비교기 잡음 등)들의 합이므로, 중심극한 정리에 의해 종모양의 분포를 가진다.
※ 중심극한 정리
여러 개의 독립적인 작은 잡음(확률 변수)들이 더해지면, 그 합은 자연스럽게 정규분포(종모양)에 가까워진다는 것임. 주사위에 비유하면 주사위 1개를 던지면, 1~6이 균등하게 나옴 (균등분포) 그런데 주사위 5개를 던지고 합을 보면, 가운데 값 근처(15)에 몰리고, 양쪽 끝(5, 30)은 드물어집니다. 랜덤 효과가 여러 개 쌓이면, 가운데 값이 제일 많고, 양쪽 끝으로 갈수록 드물어지는 정규분포가 됨.
하지만 실제 ADC의 DNL (Differential Nonlinearity)이 histogram의 Gaussian분포(종모양)에 영향을 준다. DNL은 각 코드 단계의 폭이 이상적인 1 LSB와 얼마만큼 다른지 나타내는 지표이다.
실제 ADC에는 DNL이 존재하므로 어떤 코드는 transition width가 넓어 더 자주 카운트되며, 어떤 코드는 transition width이 좁아서 덜 자주 카운트된다. 그래서 완벽한 Gaussian에서 약간 어긋날 수 있지만, 전체적으로 Gaussian분포에 가까워야 한다.
이러한 이유 때문에 σ를 한 지점의 입력 전압값에 대해서 구하는 것은 지양해야한다. 만약 DNL이 꽤 크다면 특정 DC 입력에선 σ가 작게 보일 수도 있고 다른 입력에선 크게 보일 수도 있다. 따라서 여러 DC 입력 전압에서 σ를 구해 평균을 내는 것이 ADC의 실제 input-referred noise 를 대표한다고 볼 수 있다.

다음 그림과 같이 히스토그램이 gaussian 분포를 가지지 않고, 울퉁불퉁하면 ADC 자체 설계 문제, 시스템 설계 문제(PCB 레이아웃 불량, 그라운드 분리/처리 부적절, 전원 decoupling 부족)가 있다고 판단할 수 있다.
또한 입력전압에 따라 히스토그램의 폭이 크게 달라지는 것도 문제가 있다. 정상적인 ADC라면 입력전압과 무관하게 σ가 일정해야 한다. 앞에서 언급한 열잡음, kT/C 잡음은 입력전압의 크기와 무관하게 일정한 크기의 잡음이다.
따라서 ADC의 grounded input histogram 모양이 울퉁불퉁하거나, 입력전압의 크기에 따라 폭이 달라지면, 열잡음, kT/C 잡음이 아닌 다른 요인의 영향을 받고 있다는 것이다.

3. NOISE-FREE (FLICKER-FREE) CODE RESOLUTION
Nominal Resolution가 16비트여도, 내부 잡음 때문에 모든 코드(LSB 단위)가 완전히 안정적으로 구분되지는 못함. 즉 잡음 때문에 코드가 흔들리면, LSB 단위로 식별이 불가능하다. 그래서 잡음을 반영하여 실제로 구분 가능한 비트 수를 Noise-Free Code Resolution이라 함.
예를 들어 16-bit ADC이지만 input-referred noise가 2 LSB rms이면, ADC의 실제 분해능이 16비트보다 낮을 수 있음. 잡음 없는 것처럼 보이는 유효 비트가 Noise-Free Code Resolution임.
RMS noise × 6.6 = Peak-to-Peak Noise, RMS 잡음을 Peak-to-Peak 잡음으로 바꿀 때 6.6을 곱한다. 왜 6.6인가? 정규분포에서 ±1σ 은 전체의 68% 범위를 포함하며, ±3.3σ이 99.9% 이상 범위를 포함하는 값임. 따라서 거의 모든 코드가 들어가는 peak-to-peak 유효 잡음 폭이 RMS noise × 6.6 임.
Noise-Free Counts는 전체 코드 개수를 잡음이 차지하는 LSB 폭으로 나눈 값으로 다음과 같다.
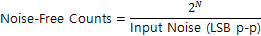
잡음 폭이 넓을수록 구분 가능한 안정 코드 수는 감소한다.
비트 단위로 변환하면

이다.
예를 들어 16-bit ADC, σ = 0.5 LSB rms이면, Noise Free Resolution은 얼마인가?
Peak-to-Peak LSB

, Noise-Free Counts

, 비트로 변환

이다. 16비트 ADC지만, Noise-Free Resolution ≈ 14.3 bit이므로 안정적으로 구분되는 건 약 14비트이다.
※ ENOB와 Noise-Free Resolution의 비교
ENOB는 AC 입력 상황에서 SNR 기준 성능평가 지표이며, Noise-Free Resolution은 DC 입력상황에서 구분가능한 코드 수를 기반으로 한 성능평가 지표이다.
Noise-Free Resolution은 코드의 안정성을 평가한다. ADC 입력에 DC(또는 매우 저주파)를 넣고, 출력 코드 히스토그램을 만든다. 코드가 흔들리지 않고 안정적으로 구분되는 비트 수가 몇 개인지 측정한다. 이렇게 샘플 간 코드가 튀지 않는지를 보는 정적(DC) 지표이다.
ENOB는 파형의 충실도를 평가한다. 고주파 AC 신호에서는 신호가 계속 변하고, 순간 값이 계속 바뀌고, 잡음도 포함되고, FFT 대역폭에 따라 노이즈 전력이 분산됨. 이런 상황에서 코드의 값이 흔들리는지는 중요하지 않다. SNR, SINAD, THD, SFDR, ENOB(AC) 같은 동적 성능 지표가 중요하다.
파형 충실도는 “ADC가 입력 아날로그 파형을 얼마나 정확하게 따라가는지”이다. 아날로그 입력 신호 → 디지털 변환 → 다시 아날로그로 재구성했을 때, 원래 파형과 얼마나 비슷한 지 본다. 원래 신호 크기가 세세하게 얼마인지가 중요한 것이 아니라 신호의 전체적인 모양과 변화를 잘 복원할 수 있는지가 중요하다.
관련 지표로 선형성 (INL, DNL), 왜곡 (THD), 잡음 (SNR), SFDR 등이 있다. 주로 AC(시간에 따라 변하는) 신호 구분 성능을 본다 (예: 통신, 오디오, 센서에서 신호 스펙트럼 분석 등)
코드 안정성은 “입력이 변하지 않을 때, 출력 코드가 얼마나 흔들리지 않는지”이다. DC 입력(혹은 매우 느린 신호)을 넣었는데 ADC 출력 코드가 1000, 1001, 999… 왔다 갔다 하면 → 코드가 불안정하다고 한다.
코드 안정성이 좋으면, 파형 충실도 개선이 되지만, 코드 안정성과 파형 충실도는 다른 말임.
Sigma-Delta(Σ-Δ) 방식의 고해상도 측정용 ADC에는 두 가지 ‘해상도 스펙’ Noise-Free Code Resolution과 Effective Resolution이 언급된다.
Noise-Free Code Resolution는 앞에서 언급한 것처럼, 입력이 거의 고정일 때, ADC 출력이 변하지 않고, 안정적으로 유지되는 코드 수이다. 다음은 AD7730의 데이터 시트이다.

위에서 ±10 mV 입력, 출력 속도 50 Hz일 때, noise-free resolution = 16.5 bits이며, 이는 출력코드가 80,000개(80,000단계)까지 구분 가능하다는 말임.
샘플링 속도를 낮추면 평균을 더 많이 수행하여, 잡음을 낮출 수 있기에, 샘플링 속도가 낮을수록 peak-to-peak resolution이 향상된다.
칩제조사에서 Noise-Free Resolution 대신에 Effective Resolution을 언급한다. Noise-Free Resolution은 peak-to-peak noise (즉 잡음이 최대 출렁이는 범위) 기준으로 계산하며, Effective Resolution은 RMS noise 기준(평균적인 잡음 크기, 표준편차)으로 계산한다.
따라서 effective Resolution = Noise-Free Resolution + log2(6.6)≈ Noise-Free Resolution +2.7 bits 이다. 데이터시트에서 “resolution”이 Noise Free인지 Effective 인지 확인해야 한다.
4. INCREASING ADC "RESOLUTION" AND REDUCING NOISE BY DIGITAL AVERAGING
평균(averaging)으로 input-referred noise에 의한 영향을 감소하는 방법에 대해 정리한다.
잡음이 랜덤이고 독립적이면 N개의 평균은 SNR을 √N 만큼 개선한다. 16-bit ADC의 실제 noise-free resolution은 15 bits이고, 샘플링 속도는 100 kSPS라면, 평균 개수에 따라 SNR과 Noise-free bits의 개선은 다음과 같다.
평균 2개 (N=2) 속도: 50 kSPS, SNR: +3dB, Noise-free bits → 15.5 bits
평균 4개 (N=4) 속도: 25 kSPS, SNR: +6dB, Noise-free bits → 16 bits
평균 16개 (N=16) 속도: 6.25 kSPS, SNR: +12dB, Noise-free bits → 17 bits
평균을 통해 해상도를 올릴 수 있지만, 샘플링 속도는 감소해야 한다.
평균은 DNL(Differential Non Linearity)도 완화한다. DNL에 의해 ADC에 missing code가 있다고 가정하자. 예를 들어 DNL이 커서 ADC 출력 값에서 코드 값 k를 얻지 못하고, 대신 k–1, k+1이 나왔다. 이것을 평균내면 (k–1 + k+1)/2 = k가 된다. 이와 같이 평균을 통해 DNL에 의한 에러를 완화할 수 있다. 다만 INL(Integral Non Linearity)에 의한 에러는 보정할 수 없다.
잡음이 아예 없는 ADC A와 약간의 잡음이 있는 ADC B가 있다. 잡음이 아예 없는 ADC A가 ADC B보다 나을까? 평균 방법을 적용해야 한다면, 약간이 잡음이 있는 ADC B에 개선의 여지가 있다. 예를 들면 다음과 같다.
Noise-free ADC A가 있다. 입력 = 1.00000 V, LSB = 1 mV, 잡음 = 0이면, 출력 코드는 1000으로 출력된다.
1/2 LSB보다 작은 분해능으로 실제 입력값을 추정하는 경우를 보자
실제 입력이 1.0003 V이라면 이 값은 코드 경계 사이에 끼여 있다. ADC A는 1000으로 계속 똑같이 출력한다. 즉 더 세밀하게 입력 값을 읽을 방법이 없으므로 ADC의 해상도를 높일 여지가 없다.
하지만 조금의 잡음이 있는 ADC B가 있다. 입력 = 1.0003 V, 잡음 = ±0.5 mV 정도라면, 어떤 샘플은 코드 1000이고 어떤 샘플은 코드 1001로 랜덤하게 나온다. 그리고 두 코드의 발생 확률이 입력 전압을 반영한다.
아무래도 1000이 실제 값에 가깝기 때문에 1000이 나올 확률이 1001보다 높다. 1000이 70번 나오고, 1001이 30번 나왔다면, 이것을 평균하면 1000.3이 된다. 이와 같이 정수 코드보다 더 미세한 정보를 얻을 수 있다. 약한 잡음이 입력을 dithering을 하여, 평균으로 해상도를 증가시킬 수 있는 여지가 생긴다
잡음이 아예 없으면 averaging으로 더 높은 해상도를 못 얻는다. 하지만 아주 약간의 noise(dither)가 있으면 평균값이 더 미세 정보를 담을 수 있다.
5. DON'T CONFUSE EFFECTIVE NUMBER OF BITS (ENOB) WITH "EFFECTIVE RESOLUTION" OR "NOISE-FREE CODE RESOLUTION"
ENOB는 동적(AC) 성능 지표이다. Full scale 사인파를 입력하고, FFT 분석 방법으로 신호 대 잡음 +왜곡 비(SINAD)를 구한다. 이 지표에는 input referred noise, 양자화잡음, 왜곡(THD)의 영향이 모두 포함되어 있다.
Effective Resolution는 정적(DC) 성능 지표이다. 코드 히스토그램을 통해 얼마나 작은 신호까지 안정적으로 구분 가능한지. 코드가 튀지 않고 안정적으로 유지되는지를 Noise-free code 변화량으로 측정한다. 양자화 잡음은 포함되지 않는다(양자화 잡음은 ADC가 DC가 아닌 AC 신호를 샘플링하여 발생하는 잡음).
6. USING NOISE DITHER TO INCREASE ADC SPURIOUS FREE DYNAMIC RANGE
ADC에서 SFDR(Spurious-Free Dynamic Range)을 개선하기 위해 ‘dither(잡음)’을 넣는 이유와 방법을 설명하는 내용이다. SFDR은 입력 사인파 대비 가장 큰 spurious(고주파 잡음 톤)의 크기 차이(dB)이다. 즉 입력 사인파가 얼마나 깨끗하게 보이는지, 왜곡 성분이 얼마나 작은지를 보여주는 지표이다.
SFDR의 성능에 영향을 주는 2가지 원인이 있다.
Front-End 회로의 왜곡 - 입력 버퍼, sample-and-hold 등에 의한 비선형, 고조파 발생, 이 부분은 외부 요인을 추가하여 개선하기 어려움
Encoder(양자화기) 자체의 비선형성 - 실제 코드 간격이 완벽하지 않음, DNL/INL 에러로 인해 미세하게 계단 폭이 들쭉날쭉하다. 이것은 dither로 개선 가능하다.
Dither는 ADC 입력에 소량의 노이즈를 일부러 섞어서 양자화 잡음과 입력 신호의 “상관관계”를 깨뜨릴 수 있다.
입력신호가 일정한 정현파이고, 샘플링 클럭이 이상적이라면, 양자화 잡음이 랜덤이 아니라 입력신호와 상관 관계를 가지게 되어, 규칙적인 패턴이 된다. 그 결과, 잡음이 스펙트럼에 tone 형태로 나타나고, spurious가 증가한다. 이로 인해 SFDR이 나빠진다. 특히 입력 주파수와 샘플링 주파수의 비가 정수인 경우 더 나빠진다.
dither를 더하면, 노이즈가 양자화 순간마다 랜덤성을 주기 때문에 양자화 잡음이 랜덤 분포가 됨. Tone 형태의 spurious가 잡음 바닥에 흩어져 사라짐. SFDR은 증가하고, SNR은 유지되거나 약간 감소함. dither의 크기는 보통 ½ LSB rms 정도가 적당하다.

대부분 시스템은 이미 노이즈(ex ADC 자체의 input-referred noise)가 있어서 추가 dither가 필요 없다. 만약 dither를 추가하기 위해, 1 LSB 이상의 노이즈를 넣으면 SNR이 비례적으로 나빠지고 더 이상 SFDR 개선도 없다.
Dither 추가하면 SNR이 감소할 수 있다. 이것을 최소화하기 위한 방법이 random number generator, DAC를 이용하는 것이다. pseudo-random number를 생성하고, DAC로 아날로그 신호를 생성하여, 입력에 더한다. 그리고 샘플링 된 값에서 동일한 random number를 뺀다.
SNR 감소를 최소화하며 Dither의 효과를 얻을 수 있다, 하지만 Dither의 신호가 클수록, 입력가능 신호의 크기가 감소하는 단점이 있다.
Dither는 ADC 내부 코드 변환 과정에서 생긴 왜곡은 개선할 수 있지만 ADC 내부 회로의 자체 왜곡은 개선하지 못한다.
ADC 내부 회로의 자체 왜곡은 ADC의 입력 버퍼, 드라이버 앰프, 샘플앤홀드(S/H), 회로, 입력 스위치의 트랜지스터 비선형성, finite bandwidth, slew rate 제한, 입력 전압에 따른 gain 변화에 의해 생긴다. 아날로그 신호 자체가 이미 왜곡된 상태에서 샘플링 됨(S/H 회로에 입력됨). 이미 신호
자체에 고조파(2nd, 3rd harmonic 등)있는 상태이므로 Dither는 이 왜곡을 개선할 수 없음.
ADC 내부 코드 변환 과정에서 생긴 왜곡은 flash ADC의 비교기 어레이, SAR ADC의 DAC의 내부 레퍼런스, 코드 간격 불균일로 생긴다. 전압(입력신호) ↔ 디지털 코드 변환 결과가 이상적 계단이 아님. DNL (Differential Non-Linearity), INL (Integral Non-Linearity) 에러가 생김. 그 결과 특정 코드 근처에서 비선형 성분이 증가하여, spurious 발생
Dither는 코드 변환 과정의 양자화 에러를 랜덤화 함. 고조파 톤 → 넓게 퍼진 잡음 바닥으로 변환하여 SFDR 개선할 수 있다.
지금까지 소개한 Dither 입력 방식은 broadband noise (전 대역 잡음)를 넣는 것이다. 양자화 잡음이 랜덤화 되지만, 하지만 SNR이 전반적으로 나빠진다. 그래서 다음 그림과 같이 잡음을 신호 대역 밖에 아주 좁은 대역으로 DC 또는 fs/2 근처에 넣는다. Dither가 아주 좁은 대역만 차지하므로, SNR 감소가 거의 없다. Dither신호가 입력 신호 대역에 있지 않아도 ADC의 코드 변환 과정의 양자화 에러를 랜덤화 할 수 있다.

다음 그림은 파이프라인(Subranging)구조의 AD6645 (14bit, 105MSPS)이다. dither를 이용하여 DNL오차가 개선하는 예시이다.
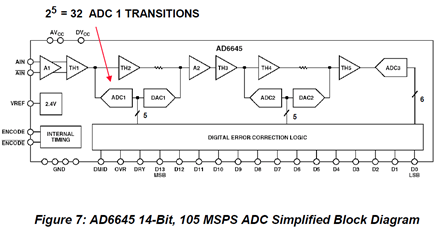
Pipeline(Subranging) ADC 구조를 가진 AD6645는 한 번에 14bit를 변환하지 않고, 3단계로 나누어서 변환한다. 1단(ADC1: 5bit)에서 대략적인 상위비트를 결정하고 나머지 2단(ADC2: 5bit), 3단(ADC3: 6bit)에서 구간 사이의 비트를 세밀하게 결정한다.
가장 큰 DNL 오차는 1단계 ADC1의 코드 경계에서 발생한다. ADC2, ADC3의 DNL 오차는 작다. ADC1은 입력 신호를 큰 step 단위로 나누므로, 다른 구간(ADC2·ADC3가 맡은 부분)에 비해 DNL 오차가 크다. ADC2·ADC3가 맡은 부분은 ADC1에서 결정하고 남은 잔차 부분을 변환하기 때문에 오차가 작다.
실질적으로 DNL 에러의 대부분은 ADC1 때문이다. ADC1은 5bit로 가능한 코드 개수 = 2⁵ = 32개이다. 즉, 입력 범위가 32개의 큰 구간으로 나뉨. full scale 입력신호 크기가 2.2 V이면, ADC1이 분할한 step 크기는 2.2 V/32≈ 68.75 mV이다. 68.75 mV 간격마다 ADC1이 변환한 코드 경계가 하나씩 있다. 이 값은 2^(14-5) = 512 LSBs에 해당한다. ADC1 코드 변환 경계는 512 LSB이며, 이 경계에서 DNL 오차는 다른 구간에 비해 크다.

입력이 특정 전압 근처(512 LSBs)일 때, 오차가 ‘고정된 방향으로’ 반복적으로 발생한다. 이로 인해 FFT를 했을 때, spurious tone 신호가 나올 가능성이 높다.
Dither를 추가하여 ADC의 입력에 특정 입력 전압(512 LSBs)이 걸리지 않도록 랜덤화를 한다. Dither의 크기가 너무 적으면 효과 없으며, 크기가 크면 SNR 손실만 커진다. 따라서 dither의 최적 크기를 찾는 것이 필요함. dither를 어느 정도 크기로 넣어야 에러의 영향을 개선할 수 있을까?
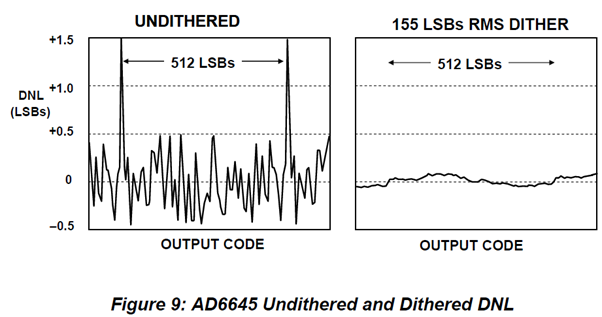
위 그림에서 Dither가 없는 경우 DNL이 512 LSB 간격으로 높은 지점이 있다. Dither 추가 후
DNL peak 부분이 사라진다.
AD6645에서 dither noise의 peak-to-peak 크기가 ADC1이 나누는 코드 간격(512 LSB)의 2배인 1024 LSB되어야 한다. 입력전압이 Dither noise에 의해 ADC1의 구간 1개를 충분히 넘나들 수 있게 된다.
dither에 의해 입력신호가 DNL 에러가 큰 특정 transition 위치에 고정되지 않고, 계속 이동하는 효과가 있어서 DNL 에러에 의한 spurious성분이 고르게 펴진다.
peak-to-peak gaussian noise는 6.6으로 나누면 rms noise이다. 1024 LSB p-p / 6.6 ≈ 155 LSB rms dither의 rms 잡음 크기는 155 LSB rms이며, 이것은 2.2 V full-scale 입력 신호 기준으로 -20.6dBm 정도이다.
다음 그림은 AD6645(파이프라인 ADC)에 out-of-band dither noise를 넣어서, SFDR이 92 dBFS → 108 dBFS로 16 dB 개선된 사례이다. 입력 신호는 –35 dBm, 30.5 MHz이며, 샘플링 주파수는 80 MSPS이고 1,048,576-point FFT로 스펙트럼을 표시하였다.

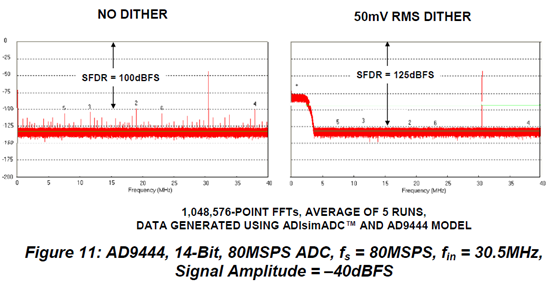
다음 그림은 AD9444 (14-bits @ 80MSPS)에 dither의 유무에 따른 스펙트럼 결과이다. SFDR이 25dB 향상된 것을 확인할 수 있다.
하지만 out-of-band 방식으로 dither 넣는다고 항상 SFDR가 좋아지는 건 아니다. dither가 개선하는 영역은 ADC 내부 코드 변환 과정과 연관된 DNL 에러, 양자화 오차에 의한 spur 부분이다. 또한 dither의 크기 고려가 필요하다. 작으면 DNL을 랜덤화 못한다. 반대로 크면 SNR 나빠지며, 입력가능한 신호의 전력이 감소하게 된다.
그리고 AC 입력 신호가 Full-Scale에 가까우면, 입력신호가 ADC 출력코드의 최저 값부터 최고 값까지 출력한다. 이 경우 INL이 지배적인 왜곡이 됨, DNL과 달리 랜덤화해도 사라지지 않음.
※ Dither가 INL 에러를 개선할 수 없는 이유
DNL 왜곡은 입력 신호가 특정 코드 경계를 지날 때 오차가 나타난다. Dither를 추가하여 이런 특정 코드의 경계를 지나가는 것을 확률적으로 분산시킬 수 있다. 하지만 INL 왜곡은 모든 샘플이 이미 비 선형적인 전송곡선을 따라가 있는 상태이다. Dither는 비 선형적인 전송 곡선을 분산 킬 수 없다.
ADC의 코드 변환 전송특성이 선형이 아니라, 곡률을 가진 비선형이라고 보자. x(t) = A·sin(ωt) 사인파를 입력시키면, 비선형이 있는 ADC의 출력은 y(t) = a1·x(t) + a2·x(t)^2 + a3·x(t)^3 + ... 이 된다. 출력의 거듭제곱 신호에 의해 고조파가 생긴다.
이러한 변수들이 있기 때문에 ADC의 입력에 dither를 추가할 때, 칩 제조사의 데이터시트 내용을 자세히 읽어야 한다. 어떤 상황에서 dither를 추가하여 성능 개선을 하였는지, 또는 권고사항을 확인해야 한다.
7. SUMMARY
본 글에서는 평균과 Dither라는 방법으로 ADC의 성능 개선에 대해 다루었다. 평균 방법은 DNL 에러로 인한 특정 출력 코드 값이 건너 띄어지는 상황을 개선할 수 있다. 또한 입력에 약간의 잡음이 있는 상황에서 ADC 출력 코드 값의 분해능을 높일 수 있다.
Dither는 약간의 잡음을 입력에 일부러 넣는 것이다. 이를 이용하여 양자화 잡음과 입력 신호 간의 상관관계를 깨뜨려서 spurious 성분을 줄이고 SFDR을 개선한다. Dither는 ADC 내부 자체의 왜곡은 개선할 수 없고, 코드 변환 과정에 에러와 연관된 DNL, 양자화 오차에 의한 왜곡을 개선할 수 있다.
평균과 dither는 ADC의 성능을 무조건 개선시키는 것은 아니며, ADC의 구조와 동작상황에 따라 개선 효과가 다르다.
'ADC' 카테고리의 다른 글
| DNL(Differential Non Linearity),INL(Integration Non Linearity) of ADC (0) | 2025.12.22 |
|---|---|
| Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR (MT-003) (0) | 2025.12.20 |
| Nyquist criterion (MT-002) (0) | 2025.12.17 |
| ADC SNR, 양자화 잡음(MT-001) (0) | 2025.12.15 |
| ADC 열잡음, 커패시터, 전력, ENOB (0) | 2025.12.10 |