Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR
so You Don't Get Lost in the Noise Floor (MT-003)
본 내용은 아날로그 디바이스의 MT-003 “ Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so You Don't Get Lost in the Noise Floor” 문서를 정리한 것이다.
1. 개요
ADC 성능을 숫자로 비교할 때 자주 쓰는 6가지 지표가 있다. SINAD (signal-to-noise-and-distortion ratio), ENOB (effective number of bits), SNR (signal-to-noise ratio), THD (total harmonic distortion), THD + N (total harmonic distortion plus noise), and SFDR (spurious free dynamic range). 각 지표가 무엇을 의미하는지 뿐만 아니라, 각 지표 간에 서로 어떻게 연관되는지 알아야 한다

ADC 성능 측정은 기본적으로 FFT 기반으로 수행된다.
ADC의 노이즈·왜곡을 FFT로 어떻게 측정하고, 왜 FFT 결과의 noise floor가 SNR보다 훨씬 낮게 보이는 걸까?
FFT의 FFT 크기가 M이면, 출력 스펙트럼 포인트 수는 M/2이다. 실수 신호이므로 양의 주파수만 의미 있다. FFT가 보여주는 주파수 범위는 DC ~ fs/2 (Nyquist 대역)이며, 주파수 간격(= bin width)은

이다.
SNR 정의에서의 노이즈는 DC ~ fs/2 전체 대역에 걸친 노이즈이며, FFT 결과 1개 bin의 노이즈는 fs/M 대역폭만의 노이즈임. 전체 노이즈가 M/2개의 bin으로 나뉘므로 bin 안에 있는 noise가 전체 노이즈보다 작아진다. Noise가 작아졌기 때문에 Gain이 생긴 것으로 볼 수 있기 때문에, 이것을 FFT Process Gain (처리 이득)이라 한다.

이다.

아날로그 스펙트럼 분석기에서 RBW(Resolution Bandwidth)를 줄이면, Noise floor가 내려가는 것 같은 효과이다.
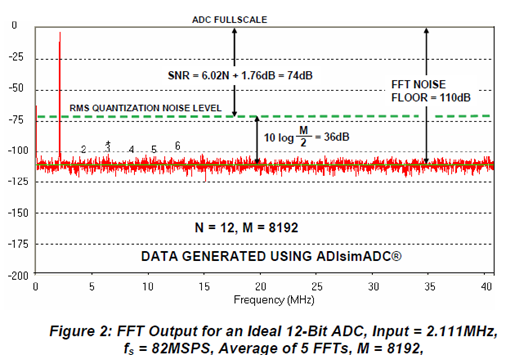
FFT를 이용해 ADC의 고조파 왜곡(harmonic distortion)을 어떻게 식별하고 측정하는가?
FFT는 디지털 스펙트럼 분석기로, FFT 출력은 아날로그 스펙트럼 분석기처럼 각 주파수 성분(신호, 고조파, 노이즈)의 크기를 측정할 수 있다. 스펙트럼은 크게 3가지 부분으로 나눌 수 있다.
1. 가장 큰 Peak값 → 기본파,
2. 그 외 규칙적으로 나타나는 Peak 값 들 → 고조파(Harmonic 파),
3. noise floor
Harmonic의 위치는 예측이 가능하다.
입력 신호 주파수
![]()
의 정수배( 2차:
![]()
,3차:
![]()
… ) 신호 는 다음 공식에 따라 위치한다.
Aliasing된 고조파 위치 공식
![]()

: 샘플링 주파수,
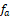
: 입력 신호 주파수,

: 고조파 차수 (2, 3, 4…),
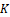
: 정수 (0, 1, 2, …)
1st Nyquist 대역을 넘어가는 Harmonic의 주파수는 접혀서 다시 0 ~ fs/2 대역으로 alias로 나타난다.
왜 데이터시트에는 2차·3차 harmonic distortion만 있나? 일반적으로 2차, 3차 고조파가 가장 크다. 그래서 대부분 ADC 데이터시트는 HD2, HD3 만 명시하며, 일부는 “Worst Harmonic” (가장 큰 고조파 하나)만 표시
그렇다면 HD(Harmonic distortion) 단위는 무엇인가? dBc로, dBc = carrier(기본파) 대비 dB이다.
예: 기본파: 0 dBFS, 2차 고조파: −65 dBc, → 기본파보다 65 dB 작다
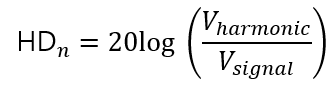
Harmonic Distortion 측정 시 입력신호의 크기를 full-scale로 하는 경우와 작게 입력하는 경우가 있다.
왜 HD는 full-scale 근처에서 측정하는 것인가? ADC 비선형성은 신호가 클수록 두드러짐. 입력신호 크기가 FS −0.5~1 dB 정도(full-scale)이면, THD/SFDR이 최악인 조건에서 측정가능 하기 때문이다.
입력신호의 크기 작게 넣는 경우는 저 레벨 입력에서는 고조파보다 DNL(차분 비선형성) 때문에 생기는 비 고조파성 Spur를 측정하기 위함이다.
큰 신호 → 고조파 왜곡(HD), 작은 신호 → DNL spur, idle tone

THD (Total Harmonic Distortion) - mean value of the root-sum-square of its harmonics
기본파를 제외한 고조파(보통 2~6차, 일반적으로 처음 5개만 중요)들의 RMS 제곱합(root-sum-square)을 기본파 RMS와 비교한 값

노이즈는 포함하지 않음, 순수한 비선형성 지표, 보통 입력신호 크기가 full-scale 일 때 측정(FS −0.5~1 dB)
THD + N (Total Harmonic Distortion + Noise) 기본파 대비 (고조파 + 모든 노이즈 성분)의 RMS 비

측정 대역폭에 따라 노이즈는 비례, 반드시 어디까지 노이즈를 포함했는지 명시해야 함.

측정 대역폭이 Nyquist BW인 경우 THD+N 와 SINAD 를 사실상 동일
SFDR (Spurious Free Dynamic Range) -신호 대비 가장 큰 스퍼(spurious tone) 한 개와의 비
Spur의 원인이 고조파인지, 클록 스퍼, IMD, DNL에 의한 것인지는 상관없이 큰 Spur와 기본파 사이의 비를 의미함.
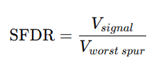
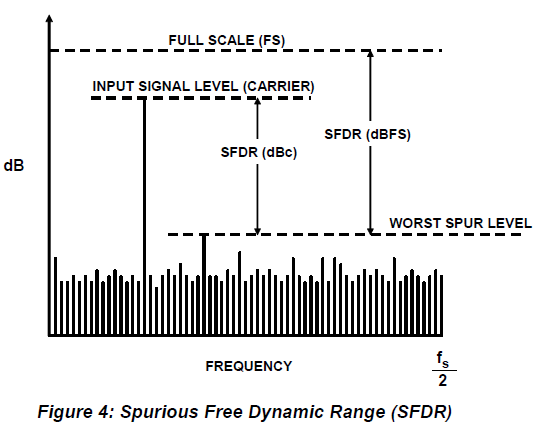
앞에서 설명한 aliasing·고조파·FFT 기반 성능지표 계산이 실제 데이터시트 그림에서 어떻게 보이는지 실제 ADC(AD9444, 14-bit 80 MSPS)로 95.111MHz 신호를 샘플링 한 것의 FFT 측정 결과를 설명한다.

95.111 MHz가 왜 15.111 MHz에 보이는가? 샘플링 주파수는
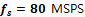
, 입력 신호

, Nyquist 주파수

, Nyquist를 초과했으므로 aliasing 발생함.

그래서 FFT에서 15.111 MHz 피크로 나타남, 기본파뿐 아니라, 2차:
![]()
, 3차:
![]()
, … 도 전부 fs/2를 초과하여, 공식
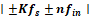
에 따라 모든 고조파가 alias 형태로 first Nyquist zone에 표시됨. 2차 harmonic인 190.22MHz가 30.22MHz에 생기고, 285.33MHz인 3차 harmonic이 34.67MHz에는 aliasing 형태로 생긴다.
※ ADC의 양자화 오차에 의해 ADC가 샘플링한 데이터의 스펙트럼에는 입력 신호 주파수의 harmonic 위치에 spur가 있다. 그 크기가 클 수도, 작을 수도 있다. ADC의 양자화 잡음이 입력신호 간 correlation 관계가 크면, 입력신호 주파수의 harmonic 위치에 있는 spur 크기가 크다. 특히 샘플링 주파수와 입력신호주파수가 정수배이면, correlation 관계가 켜져서, harmonic 위치의 spur 크기는 커진다.
2. SIGNAL-TO-NOISE-AND-DISTORTION RATIO (SINAD), SIGNAL-TO-NOISE RATIO (SNR), AND EFFECTIVE NUMBER OF BITS (ENOB)
SINAD ↔ THD+N의 관계와 SINAD가 ADC의 왜 대표 성능 지표인지에 대해 설명한다.
SINAD(Signal-to-Noise-and-Distortion)
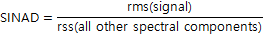
SINAD는 ADC가 만들어내는 모든 잡음(열잡음, 양자화 잡음, 모든 고조파, Spur)예 의한 영향을 한 숫자로 표현한 것이다. 또한 SINAD는 고정값이 아니다. 입력 진폭, 입력 주파수에 따라 달라짐. 다음 그림과 같이 데이터시트에 입력 진폭과 주파수에 따라 SINAD 성능이 명시되어 있음

SINAD = THD + N 인 조건, 노이즈 측정 대역폭이 DC ~ fs/2로 동일하면

입력 주파수가 높아질수록 샘플·홀드, 입력 버퍼, 스위칭 비선형성 등 때문에 왜곡이 증가, 그 결과 SINAD가 감소한다. SINAD vs 주파수 그래프는 이 ADC가 어떤 입력 주파수까지 쓸 수 있는지 보여줌
특히 ADC는 Nyquist 이하에서만 쓰는 게 아니라 undersampling 용도로도 사용됨. 이 경우 입력 주파수가 fs/2초과함. alias된 신호 품질이 중요하다. SINAD 성능은 Nyquist zone을 초과하는 입력 주파수에 대해 측정되므로 undersampling 성능을 직접 평가할 수 있다.
이상적인 N-bit ADC의 이론적 SNR
![]()
이다. 이 개념을 차용해여 SINAD 값을 이용하여 실제 ADC의 유효 비트를 표현할 수 있다.

데이터시트에 SINAD 대신 ENOB로 표현되기도 함.
SNR은 SINAD 계산 방식과 거의 동일하지만, 고조파(harmonics)를 제외하고 노이즈만 포함한다
FFT 결과로 Noise만 계산을 한다면, 기본파, DC, 1~5차 고조파를 제거하고 나머지 bin들을 노이즈로 합산한다.
SNR과 SINAD의 차이는 harmonic 성분 포함 여부임. 입력주파수가 증가하면SNR, SINAD 모두 지표가 감소한다. 하지만 SNR보다 SINAD의 지표 감소량이 더 크다. 입력 주파수가 높아질수록, 샘플/홀드 비선형성, 입력 버퍼 왜곡에 의해 harmonic 성분이 커진다. SNR은 harmonic성분을 제외한 잡음만 고려한 지표이고, SINAD는 harmonic 성분까지 고려한 지표이다. 따라서 SINAD 지표의 감소량이 더 크다. 이 차이로부터 입력 주파수가 커짐에 따라 ADC의 성능에 노이즈가 미치는 영향과 왜곡이 미치는 영향을 구분할 수 있음.
3. THE MATHEMATICAL RELATIONSHIPS BETWEEN SINAD, SNR, AND THD
SINAD, SNR, THD가 서로 독립적인 지표가 아니라, 수학적으로 연결되어 있다. 같은 조건에서 측정했다면 하나를 알면 나머지를 계산할 수 있다

본 글은 SINAD, SNR, ENOB, THD, THD+N, SFDR의 정의와 관계를 설명하였다. 이 지표들은 ADC 동적 성능을 평가할 때 가장 기본적이고 자주 쓰이는 지표들이다. 단순히 숫자만 보는 게 아니라, 데이터시트에서 어떤 정의·조건으로 측정되었는지 정확히 이해하는 것이 중요하다.
'ADC' 카테고리의 다른 글
| The Good, the bad, and the Ugly Aspects of ADC Input Noise(MT-004) (0) | 2025.12.29 |
|---|---|
| DNL(Differential Non Linearity),INL(Integration Non Linearity) of ADC (0) | 2025.12.22 |
| Nyquist criterion (MT-002) (0) | 2025.12.17 |
| ADC SNR, 양자화 잡음(MT-001) (0) | 2025.12.15 |
| ADC 열잡음, 커패시터, 전력, ENOB (0) | 2025.12.10 |