1. 개요
본 글에서는 Hamming winodow 곱의 이점에 대해 정리하였다.
2. Hamming window를 하는 이유

| 구분 | window 미적용 (Raw) | Hamming window 적용 |
| 시간영역 | 원래 신호 그대로 | 경계부 감쇠 → 왜곡 있음 |
| 주파수영역 | 스펙트럼 누출 심함 (side lobe 큼) | 누출 줄어듦 (사이드로브 작음) |
| 주파수 해상도 | 높음 | 약간 낮음 (메인로브 넓어짐) |
| 신호 진폭 | 정확함 | 보정 필요 (윈도우 에너지 때문) |
따라서 다음과 같이 쓰임
- 분석(FFT 시각화, 주파수 검출) → ✅ Hamming window 유리
- 정확한 파형 복원이나 IQ 연산 (예: 동기 복조) → ❌ 원 데이터 그대로 사용
예시
| % 샘플링 설정 fs = 1e3; % 샘플링 주파수 (Hz) N = 200; % 샘플 개수 t = (0:N-1)/fs; % 시간 벡터 % 신호 생성 (복소수 IQ 신호) f_sig = 121.5; % 신호 주파수 iq_data = exp(1j*2*pi*f_sig*t); % I+jQ 형태의 단일 톤 % 윈도우 정의 w = hamming(N).'; % Hamming window iq_win = iq_data .* w; % 윈도우 적용 |

121.5Hz인 신호를 1000Hz 샘플링 주파수로 200ms 수집한 IQ이다. 수집 IQ에 200ms 해당하는 window를 곱한다.
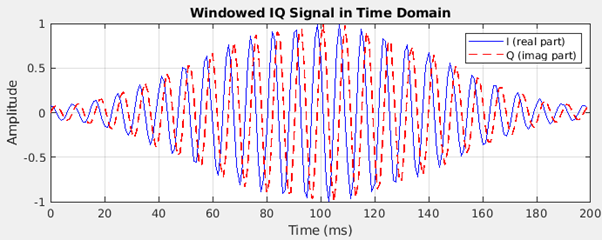
Hamming window가 곱해진 신호는 위와 같다.

원래의 IQ신호를 FFT 한 것과 Hamming window가 곱해진 IQ 신호를 FFT한 것의 결과는 위와 같다.
IQ 신호를 FFT 한 결과를 1번(파란색), Hamming window가 곱해진 IQ 신호를 FFT한 결과를 2번(빨간색)으로 명명한다.
FFT 결과에서 120Hz 부근에서 Peak점이 있다. 수집시간은 200ms이므로, FFT 분해능은 5Hz이다.
1번 결과, 2번 결과의 peak점만 보면 두 결과 모두 120Hz로 차이가 없는 것 같다.
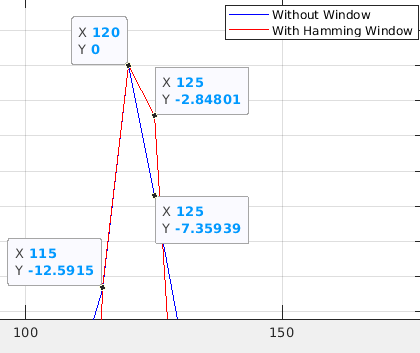
하지만 2번결과가 1번보다 우수한 점이 2개 있다.
첫번째로 120Hz 주변에서 2번 결과 side lobe가 1번 결과보다 더 작다.
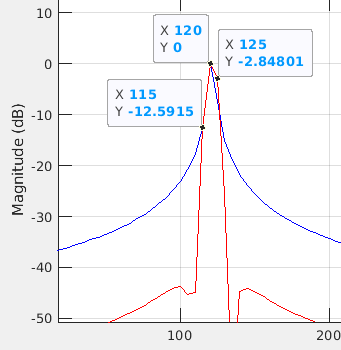
두번째로 2번결과를 이용해서 정답을 찾을 가능성이 높다. 1번, 2번 결과 모두 200ms 수집 신호를 이용하였기 때문에 FFT 분해능은 5Hz이다. 따라서 원래 정답인 121.5Hz를 정확하게 찾아낼 수 없다.
수집 시간을 늘릴 수 없는 상황에서 적용해볼 수 있는 것이 parabolic 보간법이다. 115Hz, 120Hz, 125Hz의 FFT 결과값으로 parabolic interpolation을 수행한다.

위 결과는 1번 결과로 parabolic 보간법을 수행한 것이다. 120.669Hz을 정답으로 추정한다. 정답인 121.5Hz와 0.8Hz 차이난다.
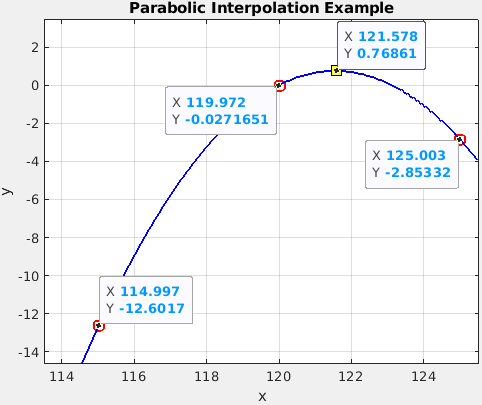
위 결과는 2번 결과로 parabolic 보간법을 수행한 것이다. 121.578Hz를 정답으로 추정한다. 실제 정답인 121.5Hz와 0.078Hz차이난다. 1번결과로 추정한 것의 오차는 0.8Hz, 2번 결과로 추정한 것의 오차는 0.078Hz이다.
즉 hamming window를 곱한 IQ의 FFT 결과로 신호의 실제 주파수를 더 가깝게 추정할 수 있다는 것을 확인할 수 있다.
'수학' 카테고리의 다른 글
| 상관과 독립 그리고 가우시안 분포 (0) | 2026.01.04 |
|---|---|
| Gauss-Markov Processes ? (0) | 2023.11.29 |
| Power spectral density과 auto correlation (1) | 2023.11.19 |
| 랜덤 process와 관련 된 용어 (0) | 2023.11.14 |
| 모멘트 (1) | 2023.11.14 |