Convolution, correlation의 식을 보고 있으면 비슷한 것 같은데, 다르다. 그리고 언급되는 곳이 다르다.
Convolution은 시스템(또는 필터)의 응답 특성 부분을 공부할 때 언급되며, correlation은 통신의 수신부분에서 언급 되며
특히 matched filter에서 많이 언급된다. Correlation은 응답특성과는 관련이 없는 것인가?
어라 어찌되었든 둘다 필터에서 쓰이는 것 같은데 왜 convolution이라는 개념이 있고, correlation이라는 개념도
따로 있는 것인가?
위와 같은 생각이 들어 correlation, convolution에 대한 개념과 그 차이에 대한 생각을 정리해보았다.
Correlation, Convolution에 대한 대략적인 느낌
▪ Correlation
두 신호 s[n], h[n]의 비슷한 정도를 표시하는데 목적을 둔 방법, 수식이다. h[n]의 시각을 옮기면서 s[n]과의 곱셈 및 덧셈을 통해 두 신호의 비슷한 정도를 구한다.
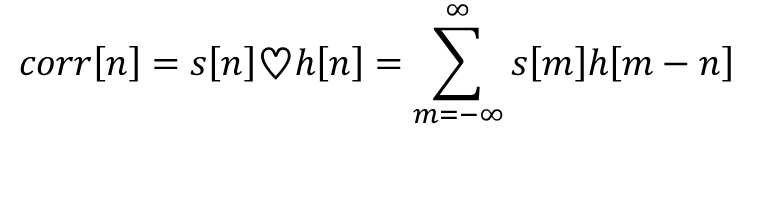
▪ Convolution
신호s[n] 시스템A의 임펄스 응답 h[n]이 있고, 시스템A에 s[n]이라는 신호를 넣으면, 시스템의 응답이 무엇인지 답을 주는 방법이다.

위와 같이 임펄스를 입력으로 주었을 때 h[n]이라는 임펄스 응답을 가진 시스템A가 있다.

시스템A의 입력에 입력 신호 s[n]을 넣으면 시스템 A의 응답은 무엇이 될까?

이것의 답을 구하는데 사용되는 수식이 convolution이다.
convolution 식을 설명할 때 s[n]을 임펄스들의 중첩으로 표현하는 것부터 시작 한다.
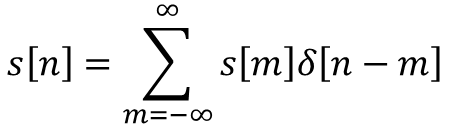
Correlation식은 shift, multiply, sum 과정을 거치지만
Convolution 식에 flip, shift, multiply, sum로 flip이 추가로 들어가는 것은 위와 같은 임펄스 표현식 δ[n-m]에서 시작
되기 때문인 것으로 보인다.
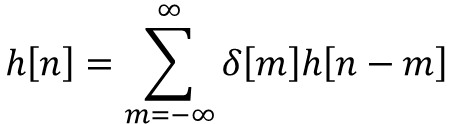
그리고 시스템 응답 s[n]*h[n]은
s[n]을 구성하는 임펄스에 대한
임펄스 응답의 중첩으로 표현된다.
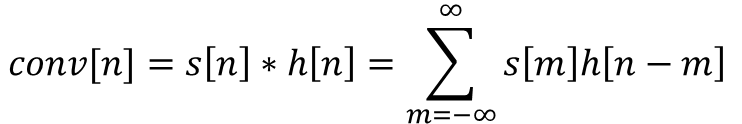
Correlation, Convolution의 계산 과정
▪ correlation
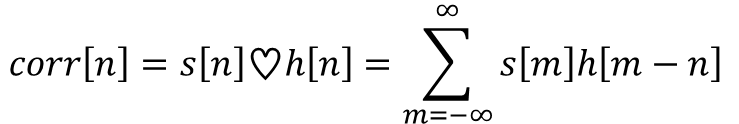
위 수식 계산을 위해 다음 과정을 거친다.
- Selecting the time shift
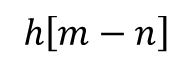
- Sample by sample product
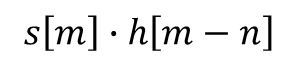
- Repeat the above process for all possible time shift n.
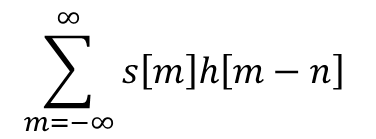
▪ convolution
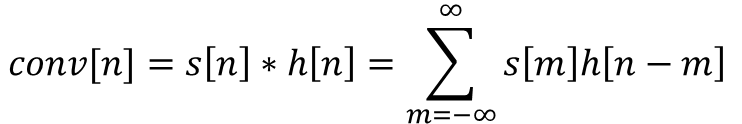
위 수식 계산을 위해 다음 과정을 거친다.
- flip
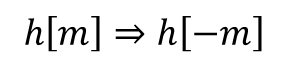
- Selecting the time shift
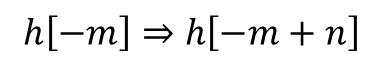
- multiply
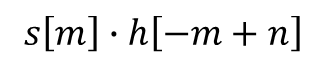
- sum

- Repeat the above process for all possible time shift n
Correlation, Convolution의 교환법칙
▪ correlation
correlation은 s[n] ♡ h[n] ≠ h[n] ♡ s[n] 임, 교환법칙이 성립하지 않음
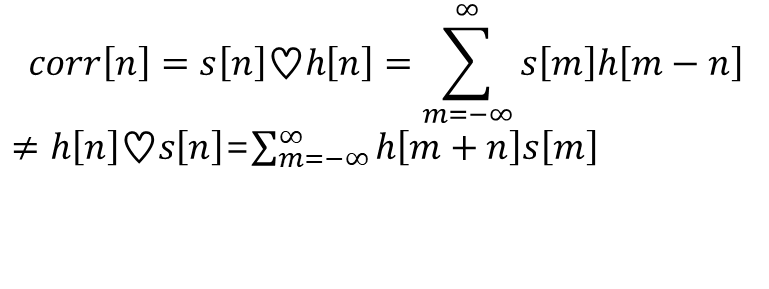
위 수식 corr[n]에 m=n+p 를 적용하면
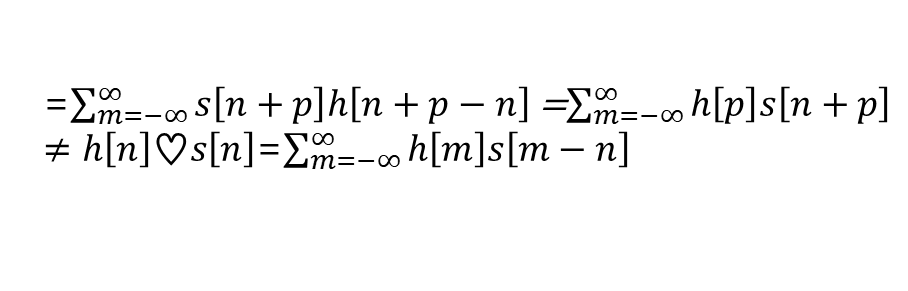
▪ convolution
convolution은 s[n]*h[n] = h[n]*s[n] 이 성립, 교환법칙이 가능함.
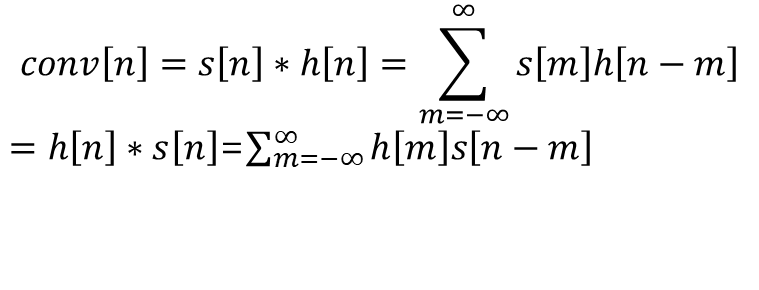
위 수식 corr[n]에 m=n-p 를 적용하면
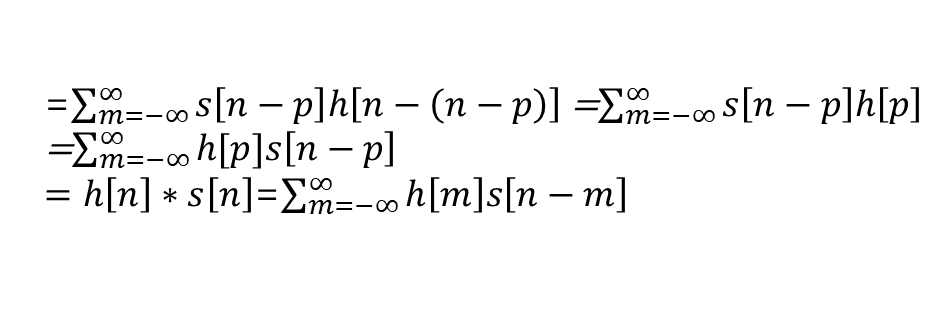
Correlation, Convolution의 복소수 계산
▪ 복소수 신호에 대한 correlation
두 신호 s[n],h[n]이 복소수라면, 두 복소수 신호의 correlation은
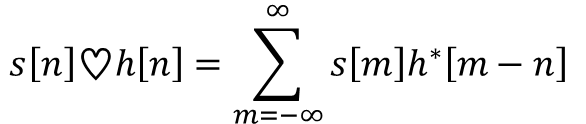
두 신호가 실수인 경우와 다른 점은 h[n]에 conjugate가 붙는다.
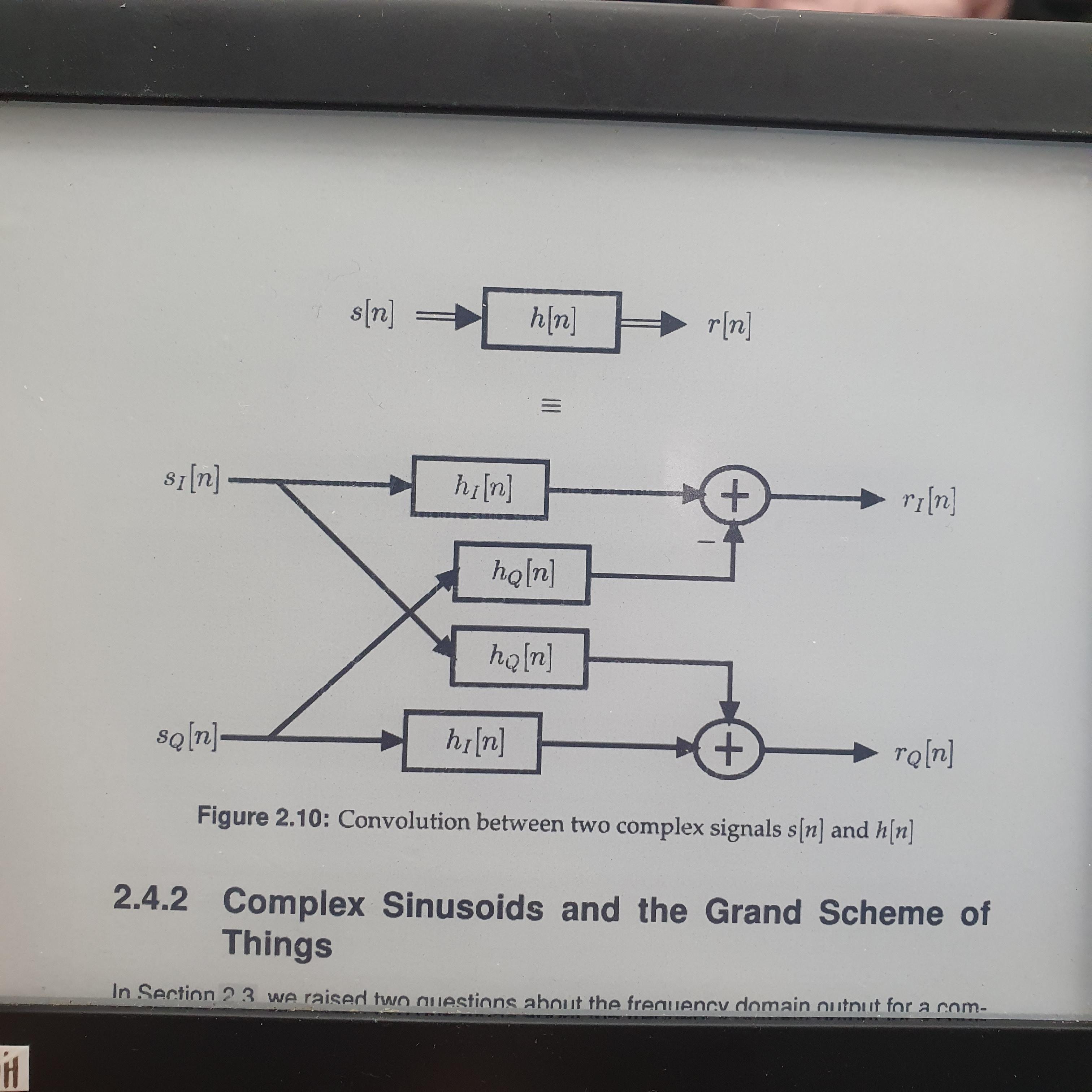
▪ 복소수 신호에 대한 convolution
convolution을 correlation으로 계산이 가능하다!?

'수학' 카테고리의 다른 글
| IQ 데이터의 스펙트럼 표시 그리고 window function (0) | 2023.09.24 |
|---|---|
| shift 연산과 folding(or flip) 연산의 정리 (0) | 2022.11.21 |
| NCO를 이용한 신호의 주파수 down convert (0) | 2022.11.05 |
| band sampling 사례, NCO 사례 (0) | 2022.10.22 |
| 내가 이해한 bandpass sampling (0) | 2022.10.10 |