band pass sampling은 왜 필요할까?
band pass sampling은 adc의 샘플링 rate(fs)보다 높은 주파수 대역에 있는 아날로그신호를
fs 주파수로 샘플링하는 것을 말한다. 이 방법의 주요 특징은 아날로그 mixer와 같이 높은 주파수 대역에 있는 아날로그 신호를 baseband로 내리면서 동시에 이산 신호를 만들 수 있다는 점이다.
bandpass 샘플링을 하는 이유로 RF 필터의 특성 때문이다. 수많은 무선신호가 있는 상황에서 사용자가 원하는 신호만 분석하기 위해서는 특정 대역만 통과시키고 나머지는 억제를 해주는 filter, 물리적으로 구현된 bandpass filter가 꼭 필요하다.
보통 bandpass filter로 saw filter가 많이 쓰이고 있다.
원하는 신호의 대역폭이 큰 경우( 수십, 수백 MHz), 그리고 날카로운 필터 특성을 만족하는 saw filter를 저주파수 대역에서는 물리적으로 구현하기 힘들다.
그래서 RF 보드의 중간주파수(IF) 선정시, mixer를 이용하여 원하는 신호를 내릴때, base band 부근이 아니라, saw filter 구현이 쉬운 주파수대역(ex. 수십 ~ 수백 MHz)으로 선정한다.
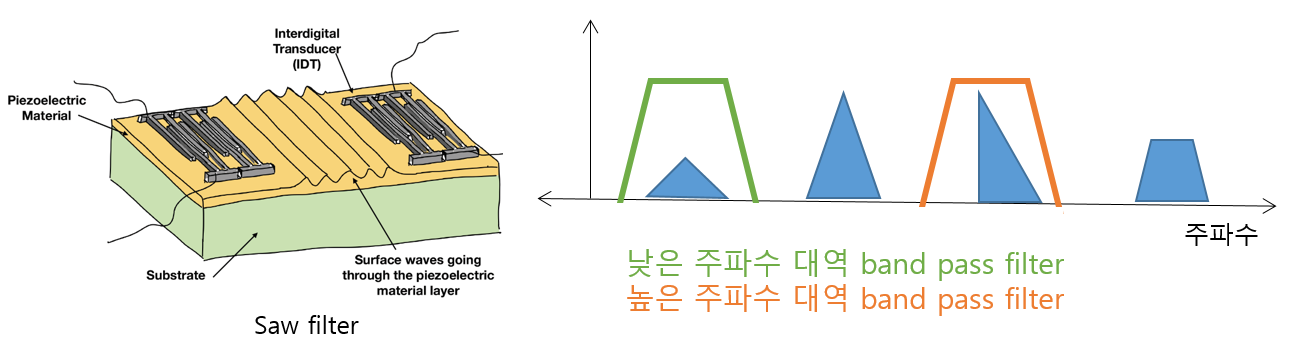
saw filter 의 그림출처 : Simulation of SAW & BAW Resonators for RF Filters | OnScale
Simulation of SAW & BAW Resonators for RF Filters | OnScale
In this blog post we discuss why engineers should be using simulation to design BAW and SAW resonators for Radio Frequency (RF) filters.
onscale.com
그 결과 RF 보드는 사용자가 원하는 신호를 base band가 아닌, 좀 더 높은(?) 주파수(IF) 대역에 내려준다.
하지만 신호 분석을 위해서는 IF 대역에 있는 원하는 신호를 base band까지 내려야 하는데 이것을 누가 해줄 것인가?
그 방법이 바로 band pass sampling이다.
Band pass sampling을 사용하는 상황을 보자.
RF 보드는 안테나로부터 RF 신호를 수신한다. RF보드는 mixer를 이용해 RF 신호를 IF 주파수 대역으로 내린다.
IF로 내린 신호를 frequency domain에서 표현하면 다음과 같다.
그 중 사용자가 샘플링하려는 신호가 샘플링 주파수 부근에 있는 신호이다.
band pass filter를 통해 사용자가 원하는 신호만 필터를 하고 샘플링을 하면 어떻게 될까?
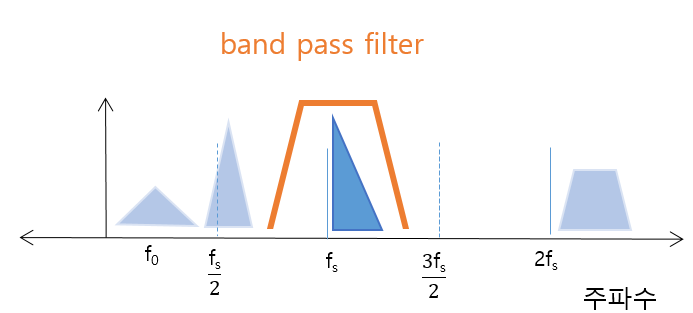
band pass filter를 거친 신호 s2(t)의 fs 부근에 있는 신호이다.

우선 filtering 한 신호 s2(t)를 Fourier Transform을 이용하여 주파수 domain에 표현하면 다음과 같이 표현된다.

filtering 한 신호 s2(t)를 fs 주파수로 샘플링하고, 샘플링 된 이산 신호를 DFT(Discrete Fourier Transform)에 넣어 주파수 domain에 표현하면....
다음과 같이 원래신호뿐만 아니라, 원래 신호의 aliasing 신호들이 반복적으로 fs 간격마다 존재한다.

초록색으로 표시된 부분과 같이, baseband 대역에 원래신호와 똑같은 신호가 존재한다.
결과적으로 band pass sampling을 통해 아날로그 신호의 주파수대역을 낮추면서 sampling을 동시에 수행할 수 있다.
'수학' 카테고리의 다른 글
| Correlation, convolution의 개념과 그 차이 (0) | 2022.11.14 |
|---|---|
| NCO를 이용한 신호의 주파수 down convert (0) | 2022.11.05 |
| band sampling 사례, NCO 사례 (0) | 2022.10.22 |
| 내가 이해한 나이퀴스트 이론 (0) | 2022.10.10 |
| 실수 신호를 복소수(I+iQ)로 만든 다음 frequency domain에 표현하는 이유 (0) | 2022.10.09 |