참고자료
http://www.panoradio-sdr.de/analog-digital-conversion/
샘플링이론
아날로그 신호를 샘플링한다면 얼마나 빠른 주기로 해야할까? 이것에 대한 답이 샤논의 샘플링 이론이다.
샤논의 샘플링 이론을 만족한다는 말은 다음과 같다.
fs > 2×f (high)
fs : 샘플링 주파수

f (high ): 아날로그 신호(샘플링의 대상이 되는)의 구성 신호들의 주파수 중 가장 큰 주파수
예를 들어
아날로그 신호 a는 다양한 주파수( f0, f1, f2,)를 가진 신호들로 구성되어 있다. f2가 가장 큰 주파수이다.
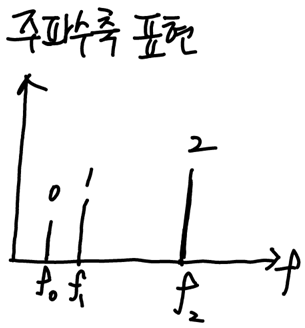
a 신호를 주파수 정보 손실없이, 시간축샘플링을 한다면 얼마나 빨리 해야할까?
위 이론에 따라 fs > 2x f2 이어야 한다.
샘플링된 디지털신호를 다시 아날로그 신호로 복원하면, 복원된 아날로그 신호는 원래 아날로그 신호가 포함하는 주파수 정보를 완벽히 가지고 있다
단 진폭은 양자화 오류때문에 원래 신호와 똑같이는 말고 비슷!하게 복원이 된다.

Aliasing
샘플링이론을 만족하지 못하는 경우 무슨일이 일어나는걸까?
즉 fs < 2×f (high) 이면, aliasing이라는 현상이 발생한다.
예를 들어
샘플링 주파수가 다음과 같고,
fs < 2×f2
fs > 2×( f0 , f1)
이런 상황에서, 신호 a를 샘플링한다면 어떻게 될까?
샘플링 된 디지털화 된 신호를 다시 아날로그 신호로 복원 하자. 복원된 아날로그 신호의 주파수 측면으로 표현하면 다음 같이 나타난다. 본래 f2에 있던 신호가 fs - f2에 위치한다.

f2 에 있었던 신호가 fs-f2에 나타나는 현상이 생겼다. 이것이 aliasing이라 하며, fs-f2를 aliasing 주파수라고 한다.
샘플링이론을 만족하지 않는 경우, [본래 f2 에 있었던 신호]가 복원된 아날로그 신호에서 [aliasing 주파수를 가진 신호]로 존재한다.
신호의 본래 주파수(f anlog)와 aliasing 주파수(f)는 다음 관계를 가진다.


Nyquist Zone
아날로그 신호를 샘플링할 때, 샘플링 이론을 만족하지 못하는 주파수를 가진 신호들은
샘플링 된 디지털 신호에 어떻게 표현될까?
이를 표현하기 위해
수학자?공학자?는
아날로그 신호를 주파수축에서 표현하고, fs/2마다 나이퀴스트 존으로 구분하였다.
다음그림에서
아날로그 신호는 3가지 주파수를 가진 신호들로 구성되어 있다.
아날로그 신호를 fs 로 샘플링하고
이 샘플링된 디지털 신호를 다시 아날로그 신호로 복원한다면
본래 두번째, 세번째 나이퀴스트에 있는 신호( fs/2보다 큰)는
복원된 아날로그 신호에서 어떻게 표현이 될까?
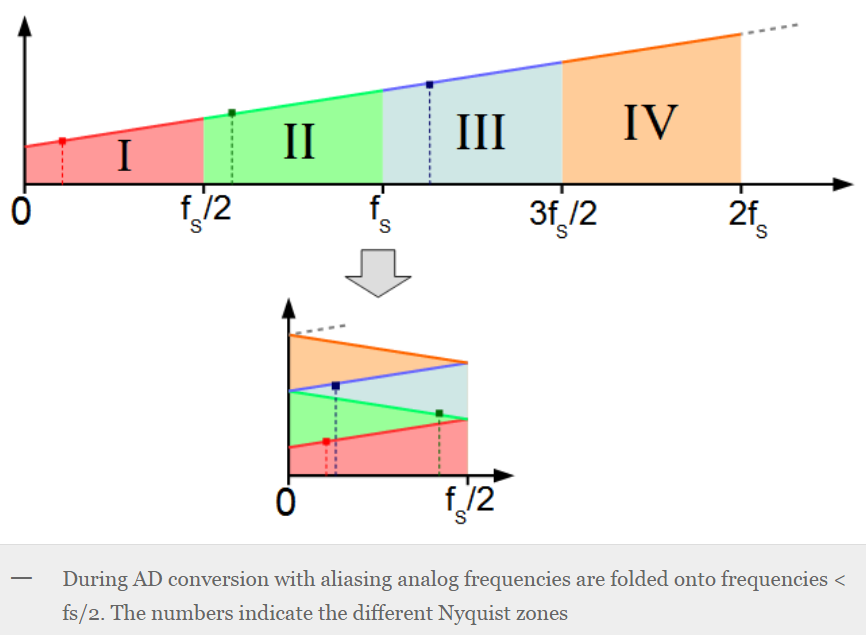

이 식의 관계에 따라
본래 두번째, 세번째 나이퀴스트에 있었던 원 신호( fs/2보다 큰)는
복원된 아날로그 신호의 주파수 측면에서, 첫번째 나이퀴스트 존에 위의 그림 같이 위치하게 된다.
아날로그 신호를 샘플링하고
샘플링된 디지털신호를 아날로그 신호로 복원하자.
샘플링 조건을 만족하지 못하는 주파수를 가진 신호들은
복원된 아날로그 신호의 주파수 측면에서 다음과 같이 위치한다.
나이퀴스트존을 기준으로 folding이 되면서 높은 나이퀴스트 존에 있는 신호들이 첫번째 나이퀴스트 존 안으로 들어온다.
'ADC' 카테고리의 다른 글
| ADC의 출력 데이터라인과 출력 클럭의 PCB line 라우팅 조건 (2) | 2023.03.31 |
|---|---|
| ADC 데이터의 검증사항 (0) | 2022.07.26 |
| 아날로그 신호를 디지털신호로 바꾼다는 것 -3 (0) | 2021.12.19 |
| 아날로그 신호를 디지털 신호로 바꾼다는 것 -1 (0) | 2021.12.19 |
| ADC의 Ground, 전류 그리고 노이즈 (0) | 2021.08.14 |