Random process
한 종류의 시험을 여러번 수행하여, 각 결과를 시간에 따라 그린 결과가 있다고 하자.
다음과 같이 시간의 변화에 따라서 첫번째 수행 결과(사건 1), 두번째 수행 결과(사건2), 세번째 수행 결과(사건3), 네번째 수행 결과(사건4)가 생긴다.

random process 는 랜덤하게 (사건)1,2,3,4가 생긴 과정을 말하는 단어이다.
한 실험을 반복해서 나온 결과는
random하게 무언가(process)를 수행되어 나온 것이기에 random process라고 용어를 만든 것 같다.
random process를 통해 생기는 (사건)의 개수가 유한개일 수도, 무한개 일수도 있다.
각 사건을 수학적으로 x(t)라고 표기하며,

사건의 모음을대괄호를 이용하여 {x(t)}로 표기한다.

확률 변수 x(t1)은
Random process를 반복하였을 때,
시각 t1에서
발생한 결과물들이다.
Random variable
위 그림 1에서 시각 t1일 때, 결과 1,2,3,4의 값들이 random variable이다. 실험을 반복하면 x(t1)은 실헐할 때마다 다른 값을 가진다.
x(t1)이라는 random variable이 특정 범위 내에 있을 확률을 probability distribution function(확률 분포 함수)로 표현할 수 있다.

확률 분포함수가 주어진다면, 확률 밀도함수는 다음과 같이 정의된다.

방금까지는 random variable[확률변수] x(t1) 1개에 대한 확률을 정의했다.
확률 변수 2개가 동시에 일어날 확률은 second order joint probability distribution function으로 수학적으로 표현한다.
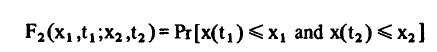
확률 변수 2개에 대한 density function은 다음과 같이 수학적으로 표현된다.
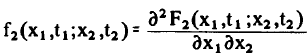
확률 변수 2개 이상에 대해서 확률 분포함수를 정의할 때에는 second order란는 용어 대신 higher order라는 단어가 붙는다.
지금까지는 2개의 random variable(확률 변수)에 대한 확률 분포함수를 수학적으로 표현했다.
2개의 random varaible말고
2개의 random process에 대한 확률 분포함수와 밀도함수를 수학적으로 표현할 수 있다.

식을 보면 x(t2) 대신에 y(t2)가 들어가 있다.
시각 t1일 때 x라는 random process의 random variable x(t1)과
시각 t2일 때 y라는 random process의 random variable y(t2)가 동시에 발생할 수 있는 확률 변수를 위와 같이 수학적으로 표현할 수 있다.
'수학' 카테고리의 다른 글
| 두 사건의 independent, exclusive에 대한 이해 (0) | 2023.11.02 |
|---|---|
| 랜덤 변수의 기대값, 분산, 상관성이라는 용어에 대한 이해 (2) | 2023.10.29 |
| 행렬의 연산과 용어에 대한 이해 (0) | 2023.10.08 |
| 측정치, 추정치, 추정치의 오차 그리고 상관계수가 1이라면.. (0) | 2023.10.02 |
| 오차의 제곱의 평균이란 (0) | 2023.10.02 |