Determinant
행렬에서 언급되는 determinant 값은
Cramer's rule을 이용하여 linear algebraic 함수의 해를 찾는데 이용된다.
하지만 최근에는 linear algebraic 함수의 해를 찾는데 반드시 determinant 를 구하지는 않는다.
determiant 값은 matrix의 invertibility가 가능한지 결정하는데 사용된다.
non singular matrix, invertible matrix, regular matrix 모두 역행렬을 의미하는 단어임.
역행렬은 원래 행렬과 곱하면, 단위행렬이 되는 행렬이다.
역행렬의 특징으로
행렬에는 여러개의 row,column이 있다. 행렬 안의 row, column 줄이 다른 row, column의 선형 결합으로 생긴 값과 같으면 역행렬은 존재하지 않는다.
또는
행렬의 determiant가 0이면 역행렬이 존재 하지 않는다.
Rank
행렬 A의 determinant가 0일 수 있지만, 행렬 A 내부에 있는 행렬 A의 크기보다 작은 행렬의 determinant가 0이 아닐 수 있다.
Rank는
모든 행렬이 determinant를 가지고 있지 않다.
행렬 A 또는 A 내부의 A의 크기보다 작은 행렬들 중에서,
0이아닌 Determinant를 가지고 있는 행렬이 있다면
그 중 가장 큰 크기를 가진 square 행렬의 dimension(크기)를 의미한다.
matrix pseudo inverse
역행렬은 보통 정사각형 행렬에서 언급되는 용어이다.
하지만 행렬의 크기가 정사각형이 아닌 경우에도 역행렬을 정의할 수 있다. 이런 경우에는 pseudo inverse matrix라고 한다.
정사각형 행렬은 방정식의 개수와 미지수의 개수가 일치하는 경우, 방정식과 미지수의 관계를 표현하는데 사용된다.
정사각형 행렬이 아닌 행렬은 방정식의 개수와 미지수의 개수가 일치하지 않는 경우의 관계를 표현하는데 사용된다.
2가지 경우를 표현할 수 있다.
1. over determined case, 미지수 개수 < 방정식 개수
이 경우 행렬A has more rows than columns
2. under determined case, 미지수 개수 > 방정식 개수
이 경우 행렬 A has more columns than rows
singular
singular 의 사전적 의미는
1. of or relating to the form of a word used when talking about one thing
2. of an unsual quality or standard; noticeable
이다.
singularity는 ' 특이점 ' 으로 언급된다.
나무위키에서는 수학적 관점에서 본 특이점을 다음과 같이 이야기한다.
"이상한 성질을 가지는, 곡선 위의 특정한 점. 이 이상한 성질이라는 것은 발산한다든지, 그 점에서 값을 지니지 않는다든지 등을 말한다. 조금 더 명확히 정의하면, 수학적인 오브젝트가 정의되지 않는 지점이다."
이런 것을 보면
singulat matrix는 역행렬이 존재하지 않거나(determinant=0), 해가 무수히 많거나, 1개의 해도 존재하지 않는 관계를 표현하는데 사용된다.
위 특성과 반대되는 관계를 표현하는데 사용하는 행렬은 non singular 특성을 가진다고 한다.
정사각형 행렬의 함수 -
정사각형 행렬이 이용되는 함수로는 1. 특성방정식, 2. 자연로그 밑의 함수 3. sin함수 4. 행렬의 exponential 이 있다.
1. 특성방정식(characteristic equation), 고유값 (eigen value)
람다: 스칼라 값
A: 정사각형 행렬

위 관계를 만족하는 함수 f(람다)를 정사각형 행렬 A에대한 characteristic equation (특성방정식) 이라고 한다.
이 특성방정식을 만족하는 값(람다)를 eigen value (고유값)라고 한다.
f(람다)는 람다의 polynomial (다항식)이다.
람다 대신 정사각형 행렬의 다향식으로 변경할 수 있다. f(A) 이다.
carely hamillton 정리에 의해서

f(A)=0 을 만족한다.

https://www.statlect.com/matrix-algebra/Cayley-Hamilton-theorem
Cayley-Hamilton theorem
Cayley-Hamilton theorem by Marco Taboga, PhD The Cayley-Hamilton theorem shows that the characteristic polynomial of a square matrix is identically equal to zero when it is transformed into a polynomial in the matrix itself. In other words, a square matrix
www.statlect.com
2,3 . 자연로그 밑의 함수와 sin함수
자연로그 밑과 sin함수를 다음과 같이 정사각형 행렬 A의 다항식으로 표현할 수 있다.


특히 자연로그 밑의 함수는 constant coefficient martix differential equation의 표현에 이용된다.
4. 행렬의 exponential
행렬의 exponential과 관련된 함수관계는 다음과 같다.

Vector-Matrix Operation
수학적인 식을 표현함에 있어서 vector와 matrix는 같이 사용된다. n크기의 벡터는 n X 1 matrix와 같다.
1. Quadratic Forms
n 크기의 vector와 symmetric(대칭)n X n의 정사각형 행렬은 스칼라 값을 정의하는데 사용된다.
vector와 행렬로 이와 같이 스칼라값을 표현하는 형태를 quadratic form이라고 한다.

2. Definite Forms
quadratic form은 행렬의 성질(definite)을 정의하는데 사용된다.

3. Norm
Vector를 normalization하듯이, Matrix (행렬)도 normalization을 할 수 있다.
Matrix normalization converts the original matrix into a normalized matrix such that the normalized matrix contains scaled values of the original matrix according to the desired range. Normalization of a vector or matrix is a common operation performed in a variety of scientific, mathematical, and programming applications.
https://blog.finxter.com/how-to-normalize-a-numpy-matrix/
How to Normalize a NumPy Matrix - Be on the Right Side of Change
In this blog post, we’ll discuss how to normalize a matrix using the popular Python library NumPy. But first things first: 👇 What is Normalization? In mathematics, normalizing refers to making something standardized or regular. Normalization of a matr
blog.finxter.com
https://mathworld.wolfram.com/FrobeniusNorm.html
Wolfram MathWorld: The Web's Most Extensive Mathematics Resource
Comprehensive encyclopedia of mathematics with 13,000 detailed entries. Continually updated, extensively illustrated, and with interactive examples.
mathworld.wolfram.com
4. Gradient Operations
Vector, 행렬을 스칼라값( ex. 시간)에 대하여 미분할 수 있다. 반대로 스칼라 함수(z)를 vector or 행렬에 대하여 미분할 수 있다.
다음과 같이
스칼라함수 z를 vector x에 대한 미분을 표현할 수 있다.


inner product를 vector에 대하여 미분한 것은

스칼라 함수 z를 vector x에 대하여 2번 미분한 것은

vector를 vector에 대해 미분한 것의 결과는 행렬이 된다.

vector x와 z의 크기가 같다면, 행렬 A의 determinant는 z의 jacobian에서 구할 수 있다.
스칼라함수 z의 행렬 A에 대한 미분을 행렬의 형태를 가지며, 다음과 같이 표현할 수 있다.

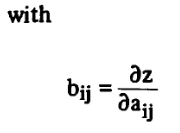
Least Squareds Techniques
행렬과 벡터는 least square 추정 기법에서 자주 사용된다.
batch processing
recursive processing
'수학' 카테고리의 다른 글
| 랜덤 변수의 기대값, 분산, 상관성이라는 용어에 대한 이해 (2) | 2023.10.29 |
|---|---|
| Random process, Random variable에 대한 이해 (0) | 2023.10.25 |
| 측정치, 추정치, 추정치의 오차 그리고 상관계수가 1이라면.. (0) | 2023.10.02 |
| 오차의 제곱의 평균이란 (0) | 2023.10.02 |
| 상관계수와 정의 (0) | 2023.10.02 |