반응형
본 내용은 APPLIED OPTIMAL ESTIMATION by Arthur Gelb 내용 중
추정치 오차의 평균이 0인 상황에서
실제값을 추정하는 경우에 대한 내용인 챕터 1장의 일부를 정리한 내용입니다.
(연습문제에서는 추정치 오차의 평균이 0이 아닌 상황에서 실제값을 추정하는 방법도 있었다.)

위와 같이 2가지 종류의 측정치로 실제값을 추정하는 상황을 보자
측정치1의 noise1과 측정치 2의 noise2가 서로 독립적, 상관관계가 0인 경우
추정치의 오차의 제곱의 평균값을 최소값이 가지도록 가중치를 측정치에 주었다면

추정치의 오차의 제곱의 평균값은
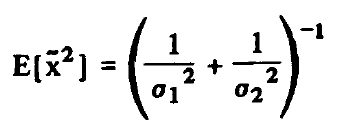
측정치로 추정한 값은

하지만
측정치1과 측정치 2의 noise가 서로 상관관계가 있다.
마찬가지로
추정치의 오차의 제곱의 평균값을 최소값이 가지도록 가중치를 측정치에 주었다면
추정치의 오차의 제곱의 평균값은


추정값은

주목할 점으로 noise1과 noise2의 상관계수가 1, -1이면
추정치 오차의 제곱의 평균값은 0이 된다는 점이다.
측정치의 noise1과 noise2의 상관계수가 0, 즉 독립적이었다면
추정치 오차의 제곱의 평균값이 0이 아니었던 것과 비교해보면 특별하게 다가온다.
위 식은
측정치1에 noise1이
측정치2에 noise2가 있는 상황일지라도, noise1과 noise2의 상관계수가 1이라면,
추정치의 오차를 0으로 만드는
추정치를 구할 수 있음을 수학적으로 보여준다고 생각하였다.
'수학' 카테고리의 다른 글
| Random process, Random variable에 대한 이해 (0) | 2023.10.25 |
|---|---|
| 행렬의 연산과 용어에 대한 이해 (0) | 2023.10.08 |
| 오차의 제곱의 평균이란 (0) | 2023.10.02 |
| 상관계수와 정의 (0) | 2023.10.02 |
| IQ 데이터의 스펙트럼 표시 그리고 window function (0) | 2023.09.24 |