1. 개요
본 글에서는 Fractional PLL의 Fractional에 대한 개념에 대해 정리한다. PLL에는 분주기가 사용된다. Fractional 분주기는 분주비를 정수뿐만 아니라, 소수점 조정도 가능하다. Fractional 분주기가 들어간 PLL은 출력신호 주파수를 소수점 단위로 조정할 수 있다.
2. 기본 PLL
① 기본 PLL의 개념 (정수 PLL)
먼저 기본 integer-N PLL 부터 보자.
- PLL(Phase Locked Loop)은 입력 기준 주파수(Reference)를 기반으로 고정 배수의 출력 주파수를 만들어내는 회로
- 일반적인 구조

- Phase Detector (PD): 입력 신호(Ref)와 분주된 피드백 신호(Feedback)의 위상을 비교
- LPF (Loop Filter): 위상 오차에 따른 제어 전압 생성 (저주파 통과)
- VCO (Voltage Controlled Oscillator): 제어 전압에 따라 주파수 변경
- ÷N Divider: 출력 주파수를 N배 낮춰 PD에 피드백
즉, 위상이 일치하면 PLL은 출력 주파수 f_out = N × f_ref 가 됨.
② Fractional-N PLL이 필요한 이유
하지만 Integer-N PLL 에서는 N이 정수라서, 다음과 같은 제약이 있다.
출력 주파수 변화 단위 = f_ref
예를 들어,
- 기준 주파수 f_ref = 10 MHz
- 분주비 N = 100
→ 출력 주파수 f_out = 100 × 10 MHz = 1 GHz
그런데 1.002 GHz를 만들고 싶다면?
- 1.002 GHz / 10 MHz = 100.2
- N = 100.2 → 정수가 아니라 불가능 ❌
즉, 주파수 분해능이 너무 거칩니다.
그래서 나온 것이 Fractional-N PLL입니다.
3. Fractional-N PLL의 핵심 아이디어
정수 N 대신 “평균적으로 N + fraction” 을 구현하는 겁니다.
예를 들어 N = 100, N+1 = 101을 아주 빠르게 번갈아가며 사용하면,
· 평균 분주비가 100.25 처럼 “소수점 값”이 됩니다.
패턴: [100, 100, 100, 101] → 평균 = 100.25
이러면 출력 주파수는:
f_out = (100.25) × f_ref
이걸 Fractional division 이라고 부릅니다.
① Fractional 분주 구현 방법
Fractional 분주를 만들려면 N을 빠르게 바꾸어야 합니다.
이를 위해 다음 회로가 사용됩니다.
I. (1) MASH (Multi-stAge noise SHaping) ΔΣ Modulator
- ΔΣ(델타-시그마) 모듈레이터가 “언제 N 또는 N+1을 쓸지” 결정합니다.
- 이 모듈레이터는 디지털 필터처럼 작동해 fraction 값을 평균적으로 유지하고,
그에 따른 양자화 잡음(Quantization Noise) 을 고주파 영역으로 밀어 올립니다. - 이렇게 하면 출력 신호의 위상 잡음이 줄고, 깨끗한 fractional 동작이 가능합니다.
② Fractional-N PLL의 수식
기본식:

- N: 정수 분주비
- K/M: Fractional 부분 (예: 1/4 → 0.25)
- f_ref: 기준 주파수
ΔΣ modulator가 분주비를 다음처럼 조정:
N, N+1, N, N+1, N, N+1, ...
그 평균이 (N + K/M) 이 되게끔 제어합니다.
③ 양자화 오차의 특징
- ΔΣ Fractional-N에서 양자화 잡음의 특징
- **양자화 오차(quantization error)**는 ΔΣ modulator에서 입력을 0 또는 1로 강제로 바꾸면서 생깁니다.
- ΔΣ 적분기의 역할:
- 결과: 저주파에서는 거의 잡음이 없고, 관심 있는 신호 대역 근처(fractional spur 근처)에서는 잡음이 최소, 나머지 고주파로 밀려나서 PLL 필터로 제거 가능.
④ 기본 PLL대비 장/단점
정수배(Integer-N) 분주기에서는 ΔΣ 같은 양자화 과정이 없기 때문에 양자화 잡음(quantization noise)이 존재하지 않습니다.
- 1️⃣ 정수배 분주기
- 분주비
 이 정수
이 정수 - 입력 클록 주파수

→ 출력 클록
- 예:



특징:
- 매 출력 클록마다 입력 클록을 정확히 N번 세기 때문에 출력 주파수에 오차 없음
- 잡음은 양자화 때문에 생기지 않고, 오직 VCO나 PLL 루프 필터, 위상 잡음 등 다른 요인에 의해 결정됨
- 2️⃣ Fractional-N 분주기와 차이
- Fractional-N에서는 목표 분주비가 정수가 아님 → ΔΣ modulator 사용
- 예:
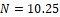
- ΔΣ는 1 또는 0으로 시퀀스를 만들어 평균이 10.25가 되도록 함
- 이때 0/1 양자화로 인해 발생하는 것이 바로 양자화 잡음
즉, fractional-N에서만 ΔΣ 양자화 잡음이 생기고, 정수 N에서는 이런 잡음이 없다.
| 항목 | Fractional-N PLL | Integer-N PLL |
| 주파수 분해능 | 매우 높음 (f_ref × 1/M) | f_ref 단위로만 변경 |
| 위상 잡음 | 높을 수 있음 (보정 필요) | 상대적으로 낮음 |
| 복잡도 | 높음 (ΔΣ modulator 등 필요) | 단순 |
4. ΔΣ 모듈레이터 구현, 적분기의 특성
Fractional 분주기에서 소수점 부분은 ΔΣ 모듈레이터로 구현된다. ΔΣ 모듈레이터 구현에 적분기가 사용된다. 1차 적분기, 2차 적분기로 구현한 것의 특성을 비교한다.
① Fractional 분주기와 ΔΣ 모듈레이터의 역할

ΔΣ modulator는 fractional control word (예: 0.25)를 입력받고,
그에 따라 분주기 제어 신호를 내보냅니다.
PLL은 평균적으로 fractional ratio를 만들어냅니다.
② 1차 적분기와 2차적분기의 차이
ΔΣ modulator는 적분기를 이용한다. 적분기를 1차 또는 2차로 구현할 수 있다. 차수가 높아지면 어떤 부분에서 차이가 있는지 정리한다.
왜 1번 적분(1차 ΔΣ)과 2번 적분(2차 ΔΣ)이 완전히 다른 분주비 노이즈 특성을 만드는가?”
- 🧠 왜 적분기가 달라지면 노이즈가 달라질까?
I. 1) ΔΣ Modulator의 구조는 “적분기 + 양자화기(1bit)”의 반복
입력 → (적분기) → (적분기) → Quantizer → 출력
여기서 적분기가 하나면 1차, 적분기가 두 개면 2차다.
- 2) 양자화기 노이즈가 존재한다
Quantizer는 아래처럼 “round or threshold” 동작을 하기 때문에
본질적으로 error = (실제 원하는 값) − (양자화된 값) 이 생긴다.
이 error가 양자화 잡음(quantization noise).
- 3) 적분기는 노이즈를 다시 처리한다
🔵 1차 ΔΣ = “양자화 잡음을 적분기 1개로 역으로 피드백”
그래서 양자화 노이즈가 FIR 필터로 보면 이런 response를 갖는다:
H1(z) = (1 - z^-1)
이 z-domain 함수의 magnitude:
|H1(e^{jω})| ≈ ω (low freq에서 거의 0)
즉:
- ω=0 부근 → 0
→ 저주파에서 노이즈 매우 작음 - ω가 증가 → 증가
→ 고주파로 갈수록 노이즈 몰림
그러니까 “노이즈를 고주파로 보내는” 효과 = Noise shaping!
🔴 2차 ΔΣ = 적분기 2개 → 양자화 노이즈 전달 함수가 (1 - z^-1)^2
2차일 때 노이즈 전달 함수:
H2(z) = (1 - z^-1)^2
Magnitude:
|H2(e^{jω})| ≈ ω^2
즉:
- ω=0 근처에서는 ω^2 → 훨씬 더 작은 값
→ 저주파 노이즈가 1차의 ω보다 훨씬 더 억제됨 - 고주파로 갈수록 더 가파르게 증가
→ 1차보다 더 많이 고주파에 몰림
그래서 2차 ΔΣ가 fractional spur 억제에 훨씬 유리.
- 🔍 직관적 비유
II. 📌 “적분기 1개 → 양자화 잡음을 한 번 누적”
→ 저주파 잡음이 일부 억제됨
III. 📌 “적분기 2개 → 잡음을 두 번 누적해서 더 부드럽게 만듦”
→ 저주파 잡음을 극단적으로 줄임
결과적으로 1차 vs 2차는 저주파 노이즈 억제 능력(=PLL Loop bandwidth 안에서의 스퍼 억제)이 완전히 다름.
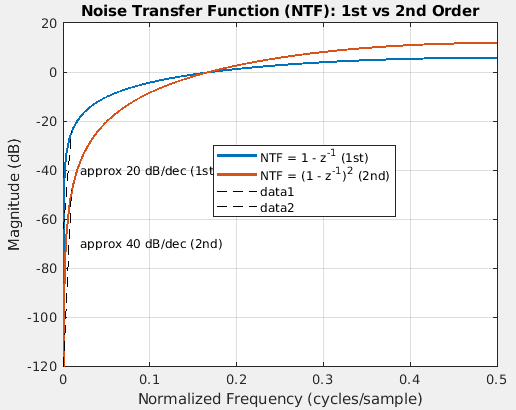
1차적분기와 2차적분기의 주파수 특성
| ΔΣ 차수 | 주파수 노이즈 특성 |
| 1차 | 20 dB/dec 노이즈 shaping |
| 2차 | 40 dB/dec 노이즈 shaping (저주파 노이즈 훨씬 적음) |
오해- 구현하려는 소수점에 따라 적분기의 응답특성이 달라지는가?
**“소수점(frac) 값이 달라져도 적분기(ΔΣ)의 본질적인 응답 특성은 달라지지 않는다.
달라지는 것은 적분기의 동작 결과로 나오는 시퀀스의 패턴이다.

fractional 값이 달라지면, 양자화 오차 e[n]의 통계적 특성이 달라짐 → 따라서 ΔΣ 출력 스펙트럼이 다르게 보임. 즉, 적분기의 transfer function이 변하는 게 아니라, 적분기 입력(에러)의 패턴이 바뀌어 전체 출력 특성이 다르게 보이는 것
- 왜 frac에 따라 noise spectrum이 달라보일까?
ΔΣ modulator의 입력은 항상 “constant fractional error”
e[n] = fractional
하지만 실제 quantizer에 의해 오차 피드백이 걸리면서 입력이 deterministic periodic sequence가 됨
예를 들어 각 fractional에서 ΔΣ 결과는:
- 0.25 → 1이 4번 중 1번 나오는 패턴
- 0.5 → 1과 0이 규칙적으로 나오기 쉬운 패턴
- 0.75 → 1이 더 많이 나오는 패턴
이러한 규칙성 때문에 오차 시퀀스가 random white noise가 아니라 quasi-periodic 이 됨.
결과:
- 어떤 fractional에서는 spur가 매우 크게 나타남
- 어떤 fractional에서는 잡음이 random-like하게 보임
- 특히 0.5는 spur가 더 강하게 생김 (최악의 경우)
- 📌 Compare to ADC delta-sigma
ADC ΔΣ는 입력이 “아날로그 랜덤 신호”라서 양자화 오차가 pseudo-white하게 됨. 하지만 Fractional-N PLL ΔΣ는 입력이 “상수”라서 양자화 에러가 구조적으로 periodic이 되기 쉬움.
→ fractional spur 발생
→ 이게 frac 값에 따라 달라짐
→ 그래서 스펙트럼도 frac에 따라 달라 보임
- 🎯 정확한 표현
I. ❌ 적분기의 응답특성이 fractional 값에 따라 달라지는 것 X
II. ✔ fractional 값이 ΔΣ에 넣는 에러 패턴이 달라져서, 결과 스펙트럼이 바뀌는 것 O
III. ✔ ΔΣ 구조가 deterministic 이기 때문에 특정 fractional에서 strong spur이 생김
- 🔧 이해를 돕는 비유
- 적분기는 항상 똑같은 성능을 가진 필터
- 하지만 그 필터에 넣는 입력 신호(= fractional error)는 값에 따라 패턴이 달라짐
- 입력 패턴이 달라지면 출력 패턴도 당연히 달라짐
- 그래서 spectrum이 frac에 따라 달라 보임
적분기 자체는 변하지 않음.
① Fractional 분주기 구현 사례
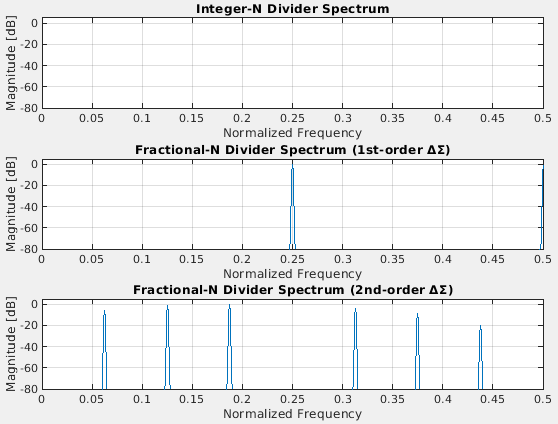
분주비를 10.25로 만드는 방법으로 정수형 분주기, 1차 적분기, 2차 적분기가 있다. 당연히 정수형 분주기는 분주비가 10으로 고정되어 있다. 1차/2차적분기를 이용한 분주기는 10과 11을 번갈아 가면서 출력한다.

분주기의 양자화 잡음 스펙트럼은 다음과 같다. Fractional 분주기의 양자화 잡음 스펙트럼은 뾰족한 spur 모양을 가진다. 정수형 분주기는 소수점 구현(N과 N+1을 번갈아가면서)을 할 수 없기 때문에 양자화 잡음과 관련 없다. 이 Spur를 줄이기 위한 방법으로 Dither가 있다.
Spur = a sharp, pointed piece of metal fixed to the boot of someone riding a horse.
Dither = to be unable to make a decision about doing something.
5. Dither의 역할
- Dither는 ΔΣ 출력 시퀀스를 “랜덤화(randomize)” 하여 deterministic periodic spur(tone 신호)가 생길 조건을 없앤다. 이를 통해 fractional spur가 사라짐.
· Dither = to be unable to make a decision about doing something.
- 출력 시퀀스를 비주기적(random-like)으로 만들어서 Deterministic periodic 성분을 없애고 spur를 broadband noise로 확산(spread)시킨다
- PLL에서는 왜 dither가 필수인가?
Fractional-N PLL에서 ΔΣ의 deterministic 특성 때문에 특정 fractional에서 spur가 엄청 크게 나타난다:
- 0.5, 0.25, 0.75, 1/3, 2/3, 등등…
이걸 없애는 가장 효과적 방법이 dither. 실제 칩(ADI, TI, Silicon Labs, Renesas)의 PLL 내부에도 Dither on/off 옵션이 거의 항상 있음.
① Fractional spur는 왜 생기는가?
Fractional spur의 근본 원인은 2가지이다.
1) ΔΣ modulator의 입력이 “상수”이기 때문 (frac = constant)
ADC ΔΣ와 달리 PLL의 fractional error는 고정값.
Ex). frac = 0.25
그러면 ΔΣ 모듈레이터는 매우 규칙적이고 반복적인 패턴을 생성한다. 0 0 1 0 0 1 0 0 1 ... 이처럼 periodic sequence가 생기면 FFT에서 narrowband tone(= spur)이 나타난다.
2) ΔΣ의 internal accumulator 가 deterministic periodic cycle에 “lock-in” 되기 때문
ΔΣ는 nonlinear system이어서 입력 frac이 어떤 rational(유리수) 값이면 내부 상태가 특정 반복 패턴에 고정됨. 이것이 fractional spur의 본질
ΔΣ(Delta-Sigma) 모듈레이터는 “적분기 + 양자화기(quantizer)” 구조인데, 양자화기(quantizer) 가 비선형(Nonlinear) 요소입니다.
y[n] = round(x[n]) 양자화기 때문에 ΔΣ 전체는 선형 시스템이 될 수 없습니다.
- frac = 0.25 = 1/4
- frac = 0.3 = 3/10
- frac = 0.125 = 1/8
이런 값들은 “유한한 분수” 입니다. 비선형 시스템에 유한한 분수비를 넣으면, 내부 상태(accumulator, integrator)의 행동이 반복 패턴에 수렴
② Dither의 구현과 역할
dither = 아주 작은 random noise를 ΔΣ modulator의 입력에 더하는 것.
수식으로: e[n] = frac + d[n], d[n]은 ±LSB의 아주 작은 random 값.
ΔΣ modulator의 입력에 Dither 신호를 더하는 것의 시뮬레이션 코드이다. ΔΣ modulator의 입력과 Dither 신호 부분을 주황색으로 표시하였다.

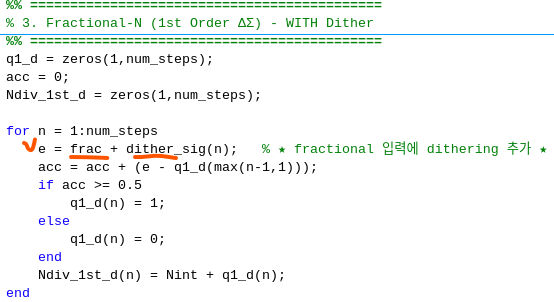
1) ΔΣ 출력 시퀀스를 비주기화(non-periodic) 한다
ΔΣ는 deterministic nonlinear system이므로 입력이 완전한 상수이면 반복 시퀀스를 만들어 spur가 생김. 하지만 dither를 넣으면: 0 0 1 0 0 1 ... → (periodic) → 0 1 0 0 1 0 1 ... (random-like)
- 더 이상 완전한 반복이 없음
- periodic component가 사라짐
- spur가 없어지고 broadband noise만 남음
2) accumulator가 lock-in 되는 것을 막음
dither가 내부 state를 흔들어주기 때문에 다음이 방지됨:
- 0.5 spur
- 1/4 spur
- fractional이 rational일 때 생기는 간섭 spur
즉, ΔΣ가 특정 반복 패턴에 “붙어버리는 것”을 방해함.
3) 양자화 잡음을 whiten 한다
원래 PLL ΔΣ 양자화 잡음은 deterministic이고, 특정 주파수로 몰리는 경향이 강함.
하지만 dither는 이를 다음처럼 바꾼다:
- deterministic → stochastic
- narrowband → wideband
결과적으로 PLL loop filter 통과 후:
- spur → 사라짐
- broadband noise만 남음
- 📈 그림으로 표현하면
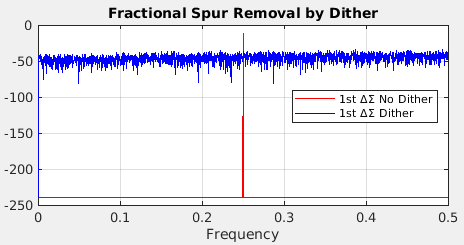
위 그림은 1차적분기로 구현한 분주기의 양자화 잡음 스펙트럼이다. Dither 신호가 없는 것은 빨간색, Dither 신호가 있는 것은 파란색이다.
Dither를 넣으면, 좁은 대역에 모인 spur가 넓게 퍼져서 wideband noise가 됨. 뾰족한 성분은 없어지지만, noise level은 올라감.
③ Dither 신호 크기에 따른 Spur 제거와 noise floor 영향
ΔΣ fractional-N PLL에서 dither amplitude에 따른 Spur 제거와 noise floor 영향을 정리하였다.
- 1️⃣ 기본 원칙
- 입력 fractional 값:

- ΔΣ 적분기 입력에 추가되는 dither:

dither amplitude
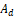
의 선택은 spur 제거와 noise floor 증가 사이의 trade off.
- 2️⃣ 크기가 frac보다 작으면
- 예: frac = 0.25, dither_amp = 0.05
- ΔΣ 내부 상태가 반복 패턴에서 완전히 벗어나지는 못하지만
- 주기적 spur가 감소하고 스펙트럼이 조금 더 균일해짐
→ 안정적이고 작은 noise floor 증가
- 3️⃣ 크기가 frac과 같거나 그 이상이면
- 예: frac = 0.25, dither_amp = 0.25~0.5
- ΔΣ 적분기에 들어가는 값이 0~0.5 정도 무작위 변화
- fractional spur는 거의 완전히 사라짐
- 대신 noise floor가 크게 올라감 → PLL phase noise 증가 가능
→ dither가 너무 크면 spur는 사라지지만 잡음이 증가
- 4️⃣ 실무에서 권장 범위
- 일반적으로 dither amplitude ≈ 0.5~1 LSB 수준
- PLL에서 LSB = 1 fractional step → dither_amp ~ 0.5 LSB 정도
- spur 제거 효과가 크면서 noise penalty가 최소화됨
- Dither 신호의 크기에 따른 영향
| Dither 신호크기 |
효과 |
| << frac | 부분적으로 spur 감소, low noise penalty |
| ≈ frac | spur 거의 제거, noise floor 증가 |
| >> frac | spur 제거 완벽, noise penalty 큼 |
'RF' 카테고리의 다른 글
| Power Spectral Density of Phase Noise and Jitter (0) | 2025.11.27 |
|---|---|
| Ublox calibration, soure measurements (0) | 2025.05.30 |
| Ublox SMGR(Sync Manger)란 ? (0) | 2025.05.28 |
| Ublox lea-m8f가 제공하는 Oscillator synchronization 구성도 (0) | 2025.05.25 |
| 왜 RF 시스템의 임피던스는 50옴 또는 75옴인가 ? (0) | 2024.08.18 |