ADC의 SNR: ADC의 신호대 잡음비는 무엇인가?
ADC는 continuous 신호를 샘플링 과정을 통해 discrete 신호로 변경한다. ADC가 출력한 discrete 신호에는 continuous 신호에 대한 정보와 잡음도 있다. 이 잡음은 어디에서 생기는 것인가?
RF 부품 SNR의 잡음 중 큰 부분을 차지 하는 것이 열잡음이다. ADC 부품에서 언급하는 잡음은 Quantization 오차에 의한 잡음이다. 다음 그림과 같이 ADC가 샘플링한 신호를 몇 비트로 표시하는가에 따라 Quantization 오차가 다르다. 높은 비트수를 사용할 수록 Quantization 오차는 줄어들기 때문에 잡음은 감소하고 ADC의 SNR성능은 높아진다.
샘플링한 신호의 전력과 Quantization 오차에 의한 잡음의 전력을 시간 영역에서 rms 값으로 계산하고, SNR로 표시하면 다음과 같다. 시간영역에서 rms 값으로 계산한 quantization 잡음전력은 q/√12이다
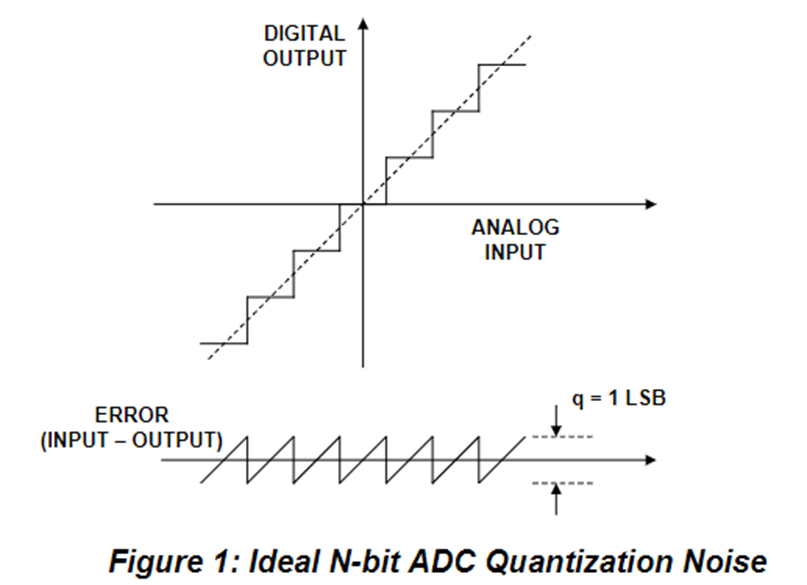

시간 영역에서 표현한 ADC 잡음 전력을 주파수 영역에서 표현하면 다음 그림과 같다. ADC가 샘플링한 신호는 continuous 신호의 fs(샘플링주파수)/2까지의 주파수 대역에 해당하는 신호 정보만 가지고 있다. 앞에서 언급한 ADC SNR의 잡음전력은 0~ fs/2까지 분포한 잡음 밀도를 전부 더한 것이다.
it is important to emphasize again that the rms quantization noise is measured over the full Nyquist bandwidth, dc to fs/2.
예를 들어 fs=100MHz인 ADC로 샘플링한 신호 중 관심 신호가 5MHz 대역폭안에 존재한다고 가정하자. 이 경우 5MHz 대역폭에 존재하는 신호의 SNR은 fs/2 대역폭에 해당하는 신호의 SNR보다 높다.
fs/2MHz 대역폭에 존재하는 총 잡음 전력보다 5MHz 대역폭에 존재하는 총 잡음 전력이 작기 때문이다.
관심 대역폭이 줄어듦에 따라 잡음전력이 더 작아지는 것을 반영한 식이 다음 그림의 process Gain이다.
fs=100MHz인 ADC로 샘플링한 신호 중 관심 신호가 5MHz인 경우 processing gain은 10dB이다.
샘플링 된 신호 중 좁은 대역폭의 신호를 볼 수록, 좁은 대역폭에 있는 총 잡음 전력이 작아진다.
관심 신호의 대역폭을 줄일 수록 관심 주파수 대역 부분 신호의 SNR이 더 커진다.
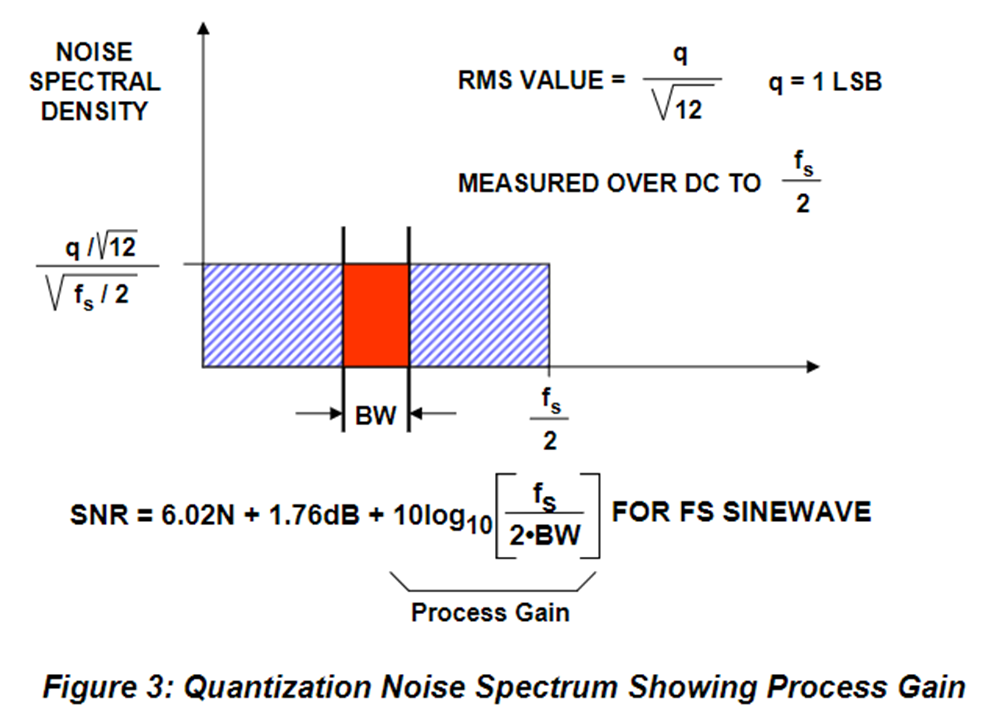
processing Gain 예시
The significance of process gain can be seen from the following example. In many digital basestations or other wideband receivers the signal bandwidth is composed of many individual channels, and a single ADC is used to digitize the entire bandwidth. For instance, the analog cellular radio system (AMPS) in the U.S. consists of 416 30-kHz wide channels, occupying a bandwidth of approximately 12.5 MHz. Assume a 65-MSPS sampling frequency, and that digital filtering is used to separate the individual 30-kHz channels. The process gain due to oversampling for these conditions is given by:
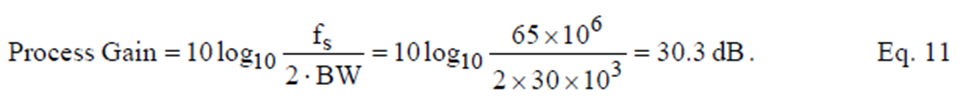
The process gain is added to the ADC SNR specification to yield the SNR in the 30-kHz bandwidth. In the above example, if the ADC SNR specification is 65 dB (dc to fs/2), then it is increased to 95.3 dB in the 30-kHz channel bandwidth (after appropriate digital filtering).
Quantization 잡음 전력과 ADC에 입력된 신호의 correlation이 된다면?
앞에서 시간영역에서 rms 값으로 계산한 quantization에 의한 잡음전력은 q/root(12)이다. 잡음전력을 계산할 때 가정한 것이 잡음 전력은 ADC에 입력된 신호와 uncorrelated되어 있다는 점이다. 하지만 샘플링 클럭과 입력된 신호는 harmonically하게 연관 되기도 한다.
샘플링은 quantization 잡음을 생성하기 때문에, quantization 잡음은 입력된 신호와 correlation 된다. 이 경우 입력 신호의 harmonic 주파수 부분에 집중 분포한다. 하지만 그런 경우에도 quantization에 의한 총 잡음전력은 대략적으로 q/root(12)이다.
The underlying assumption here is that the quantization noise is uncorrelated to the input signal. Under certain conditions where the sampling clock and the signal are harmonically related, the quantization noise becomes correlated, and the energy is concentrated in the harmonics of the signal—however, the rms value remains approximately q/√12.
출처 : MT-001 Taking the Mystery out of the Infamous Formula,"SNR = 6.02N + 1.76dB," and Why You Should Care
'ADC' 카테고리의 다른 글
| Fractional PLL의 출력 주파수를 정하기 위해 설정해야할 사항은? (0) | 2024.10.06 |
|---|---|
| Transformer에서 변압기, RF transformer, Balun, 임피던스 매칭 까지 (0) | 2024.05.06 |
| ADC의 SNR과 SFDR의 차이점 2 (0) | 2023.12.05 |
| ADC 잡음전력, 잡음과 input 신호 사이의 correlation (0) | 2023.06.12 |
| ADC 특성 중 DNL과 INL (0) | 2023.06.12 |