반응형
지금까지 정리하였던 확률용어를 통합하여 중심극한정리를 연관시킬수 있다.
https://youtu.be/fCMiq-hlUMA?si=cog9TLlC2CXqi8Oa
이 영상에서
중심극한 정리에 대해 직관적으로 설명을 해주셨다.
중심극한 정리 : 표본의 크기를 극한으로 근사시킬 때 표본 평균의 분포는 중심으로 모이게 된다.
이 영상에서 말하고자 하는 바는 다음과 같다.
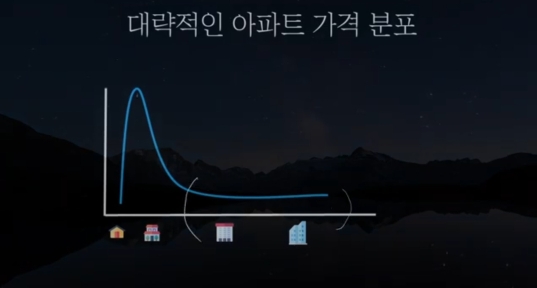
서울 집값의 분포와 위와 같다고 하자.
B 행위- 사람마다 무작위로 30개의 집을 선택하고 그것의 평균 값의 집을 살 수 있다고 하자.
위의 과정을 거치고 난 후 사람들이 산 집의 분포를 보면 다음과 같이 된다.
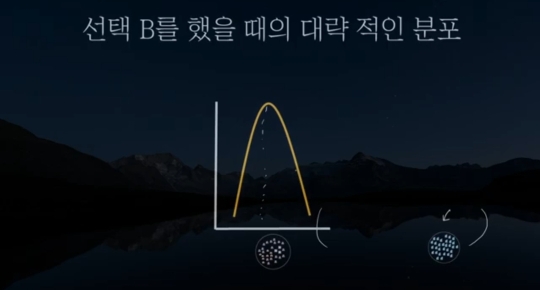
서울 집값의 분포의 그래프 형태가 좌우 대칭이 아니었다. 서울 집값의 평균값이 그래프의 중심은 아니었다.
하지만 B 행위의 결과 값의 분포는 좌우 대칭이 된다. 그리고 30개라는 표본의 크기를 키우면 키울수록 표본(B행위 결과)의 평균의 분포가 중심으로 더 밀집된다.
'수학' 카테고리의 다른 글
| 모멘트 (1) | 2023.11.14 |
|---|---|
| 랜덤변수, 랜덤프로세스 확률분포의 수학적 표현 (0) | 2023.11.12 |
| 확률 분포의 형태 (0) | 2023.11.06 |
| 두 사건의 independent, exclusive에 대한 이해 (0) | 2023.11.02 |
| 랜덤 변수의 기대값, 분산, 상관성이라는 용어에 대한 이해 (2) | 2023.10.29 |