본 글은 https://learn.wirelesspi.com/ 의 SDR course의 Linear modulation 부분을 정리하고 내용을 추가하였다.
신호 처리 자료를 보다보면 필터 관련하여 여러가지 용어들이 언급된다. 저역 통과 필터, pusle shaping filter, raised cosine filter, window 함수, black man harris, sinc 함수 등등 많다. 이런 용어들이 한꺼번에 나오니 개념이 뒤죽 박죽이 되어 서로 어떠한 관계를 가지는지 파악하기 힘들어서, 이를 정리하고자 이 글을 작성하게 되었다.
특히 pulse shaping filter의 개념을 이해하는 것이 가장 어려웠던 것 같다. pulse shaping filter도 filter인 것 같은데... Low pass filter(LPF)인지, band pass filter(BPF)인지, high pass filter(HPF)인지 어떤 범주에 속하는 것이지 잘 몰랐었다. 개념이 참 안 와닿았다.
우선 pusle shaping fiter는 filter가 맞긴 한데, LPF, BPF, HPF의 범주에 분류하는 것보다 중요한 것이 왜 Pulse shaping filter라는 개념이 나왔는지를 알아야 한다. 디지털 통신에서 디지털변조가 끝난 신호를 아날로그 신호로 만들어서 무선, 유선상에서 송,수신할 때 필요한 개념이다.
신호가 다른 신호의 시간영역이나, 주파수영역에서 간섭을 주지 않으면서 송수신 되어야 하기 때문에 pulse shaping filter라는 개념이 탄생하였다.
- Window 함수와 filter
신호를 필터링 하고 싶다. 예를 들어 신호를 필터에 통과시켜서 저주파수 대역만 통과시키고 싶다고 하자.
그렇다면 필터의 주파수 응답이 아래와 같이 직사각형 모양인 것이 이상적일 것이다.

하지만 필터의 주파수 응답이 위와 같다면 필터의 시간 응답은 다음과 같을 것이다. 이 시간 응답은 무한대의 응답을 가진다.

사진 참고 : http://www.ktword.co.kr/test/view/view.php?m_temp1=4265
위와 같이 시간응답이 무한개인 필터를 실제로 구현할 수 없다. 그래서 시간 응답이 유한한 필터를 구현해야 한다. 구현하는 과정은 다음과 같다.
이상적인 주파수응답을 가진 필터의 시간응답에 window 함수를 곱하여, 시간영역에서 무한대인 응답을 유한하게 만든다.
시간영역에서 곱셈 연산은 주파수영역에서는 컨벌루션 연산과 같다. 따라서 생성된 필터의 주파수 응답은 다음과 같이 된다.
window 함수에는 직사각형, blackman harris, hanning, kaiser 등 여러가지가 있다. gnuradio, matlab 등에서 Low pass filter 모듈 선택시 window 함수를 선택할 수 있는데, 어떤 window 함수를 선택하는가에 따라 Low pass filter의 주파수 응답이 다르다.

- 신호 송수신시, 시간영역과 주파수영역의 간섭을 최소화 하기 위한 Pulse shaping filter
pulse shaping filter를 공부하다보면 raised cosine filter라는 용어를 자주 본다. pulse shaping filter, raised cosine filter 이런 용어들은 어떤 관계를 가지고 있는가?
디지털 통신의 과정은 다음과 같다

데이터 bit들이 modulation방법에 맞추어 심볼로 변환되고 이 심볼의 크기와 위상에 따라 아날로그 신호가 생성된다. 이 아날로그 신호를 무선이든, 유선을 통해 수신자에게 전송된다. 수신자는 수신한 아날로그 신호에서 심볼로 변환하고, 심볼로 송신자가 보낸 데이터 비트들을 알 수 있다.
조금 더 자세하게 보면

데이터를 송신시 위와 같이, 비트를 symbol로 변환 > 1:L upsampling > pulse shaping > DAC 통과
를 통해 데이터 비트를 아날로그 신호로 생성하여 송신한다.
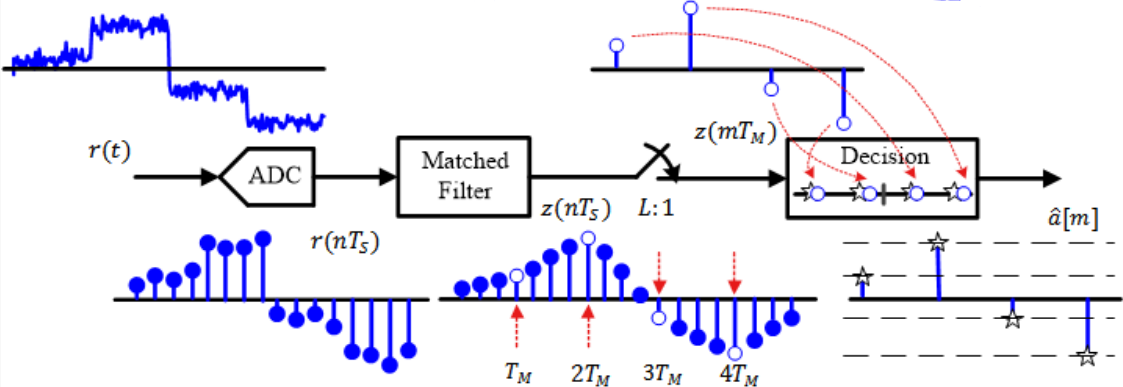
신호를 수신하는 과정은 위와 같다.
수신한 아날로그 신호 ADC 통과 > 수신한 r[n] 신호를 matched filter에 통과 > L:1 down sampling 및 symbol mapping > symbol을 bit로 변환

송신할 때 pulse shaping시 직사각형 펄스 형태의 아날로그 신호로 만들어서 송신하면 무슨 문제가 생길까 ?
직사각형 펄스 신호와 같이 시간영역에서 신호A의 크기가 급격하게 변하는 부분이 있다면, 신호 A의 주파수 응답은 다음과 같이 그 모양이 넓다. 직사각형 펄스 신호를 주파수 영역에서 보면 다음과 같다.

위와 같이 한정된 부분의 주파수 영역을 차지 하는 것이 아니라 다른 주파수 대역도 차지한다. 일상생활에서 통신사들은 각자 할당되어 있는 주파수 대역이 있으며, 다른 대역을 침범해서는 안된다.
신호 A를 그대로 송신하면 지정된 주파수 대역 이외의 다른 대역에 존재하는 신호에 간섭을 준다. 그렇다면 어떻게 해야할까?
이산신호를 아날로그 신호로 만들 때 직사각형 펄스보다 부드러운 모양의 둥글둥글하며 smooth한 펄스를 이용하는 것이다. 다음 그림과 같이 말이다.
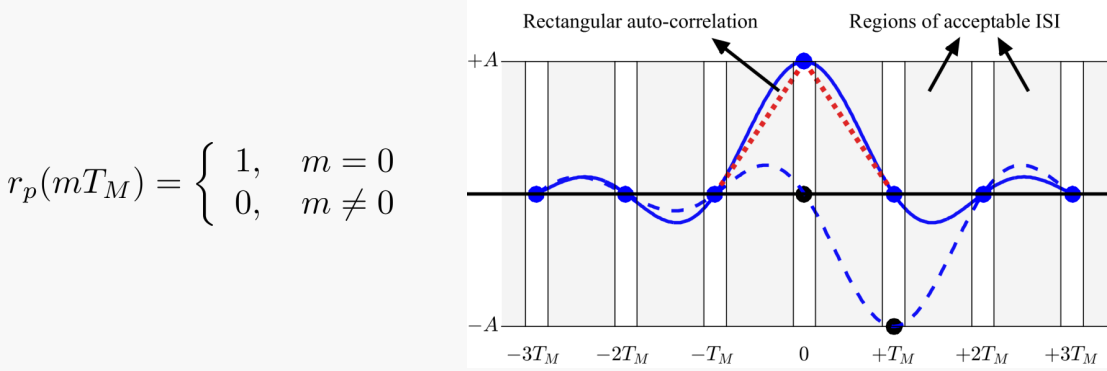
수신기가 위와 같은 수식특성과 모양을 가진 신호를 얻도록 해야, symbol을 결정할 수 있다.
위와 같은 수식특성과 모양을 가진 신호를 얻을 수 있도록, 송신부의 pulse shaping과 수신부의 matched filter를 구현해야 한다.
위와 같은 수식특성과 모양을 가진 신호(=수신부가 심볼을 결정할 수 있는 신호)가 가진 2가지 특징은
1. 한 심볼에 의해 생성된 아날로그 신호가 시간영역에서 다른 심볼의 아날로그 신호에 간섭을 주지 않는다.
2. 생성된 아날로그 신호의 주파수 응답이 다른 주파수 대역에 간섭을 주지 않는다.
두 조건을 만족하는 신호로 sinc 함수파형이 있다. sinc함수로 이산신호를 아날로그 신호로 만들었을 때 , 다른 심볼에 영향을 주지 않는다. 또한 sinc 함수가 차지하는 주파수 대역은 한정되어 있다.
하지만 !! sinc 함수는 시간영역에서 무한대응답을 가지므로 실제 구현에 사용할 수 없다.
그래서 sinc 함수의 주파수 응답을 다음과 같이 조금 늘리고, 부드러운 형태의 응답을 가진 펄스를 만드는 것을 생각하게 되었다.
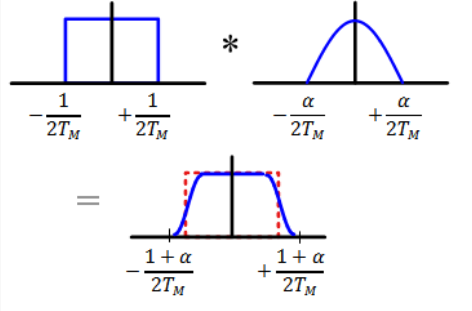
위와 같이 이상적인 주파수 응답과 cosin함수 형태를 가진 주파수 응답을 convolution한다. 생성된 펄스의 주파수 응답이 sinc 함수의 주파수 응답보다 대역이 조금 더 넓고 부드러운 형태를 가진다. 생성된 펄스를 펄스 C라고 하자.
펄스 C의 시간 응답이 수신부가 심볼을 결정할 수 있는 신호의 시간 응답이며,
펄스 C의 주파수 응답이 수신부가 심볼을 결정할 수 있는 신호의 주파수 응답이다.
다음과 같이 rolloff factor(alpha)를 이용하여 펄스 C의 주파수 응답 특성을 변형이 가능하다.
이 주파수 응답을 raised cosine 스펙트럼이, raised cosine 필터라고 한다.
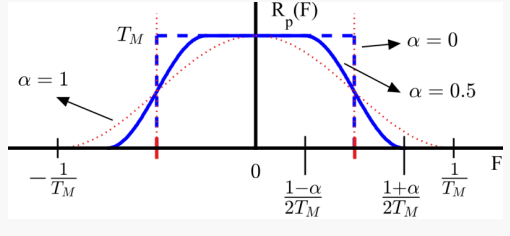
펄스 C의 시간 응답을 다음과 같이 수학적으로 표현 하며, 이것을 raised cosine 함수라고 한다.
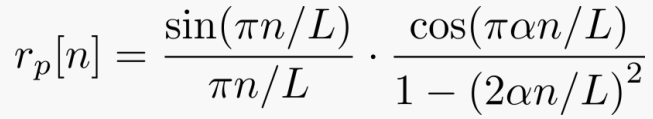
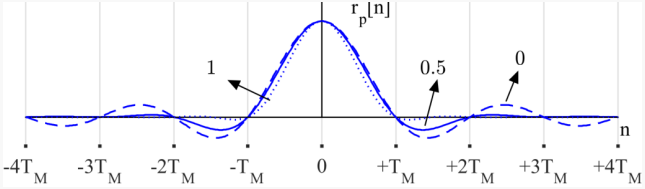
rolloff factor가 0, 0.5, 1일 때 raised cosine 함수 시간 응답의 형태는 다음과 같다.
- square root raised cosine이라는 용어 중 왜? square root라는 용어가 붙은것일까?

수신부가 심볼을 결정할 수 있도록, 심볼을 raised cosine 함수로 만들어 주는 부분을 어디에 구현해야 할까?
수신부에만 구현 : 수신부에서만 수신신호를 raised cosine 형태로 만든다고 보자.
송신 신호의 주파수대역을 보면 spectral leakage가 발생한다. 할당된 주파수대역 이외의 대역에도 간섭을 준다. 이것을 수신부가 대응을 못하게 된다.
송신부에만 구현 : 송신부에서만 심볼을 raised cosine 시간 응답형태로 만들어서 전송한다고 보자.
filter가 없는 수신부는 아날로그 신호를 수신할 때, 잡음이나 외부 간섭을 제거하지 못한다.
위의 문제를 해결하기 위해,
다음과 같이 수신부가 raised cosine 시간 응답 형태의 신호를 수신할 수 있도록 한다.
pulse shaping filter와 matched filter라는 개념을 이용하여, raise cosine 시간 응답을 TX와 RX에 나누어서 구현한다.
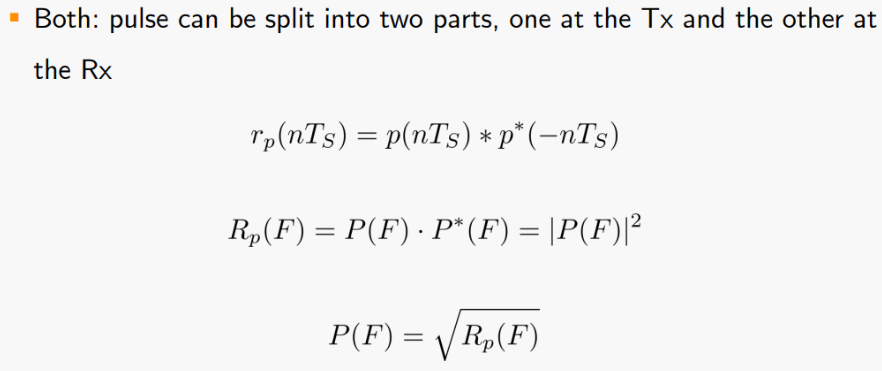
위 그림에서
r_p(nTs)는 raised cosine 함수의 시간 응답이다.
p(nTS) 부분을 송신부의 pulse shaping filter에 구현하고 p*(-nTs) 부분을 수신부의 matched filter에 구현한다.
raised cosine 함수의 주파수 응답은 R_p(F)이다.
송신부의 pulse shaping filter의 주파수 응답은 R_p(F)의 제곱근(squre root) 형태이다.
이러한 연유로 인해
송신부의 pulse shaping filter를 square root raised cosine filter라고 한다.
'Gnuradio' 카테고리의 다른 글
| DLL에 구현된 함수를 프로젝트에 import하는 방법과 구조 (0) | 2024.10.09 |
|---|---|
| DDS, NCO의 phase increment 개념 (0) | 2023.04.21 |
| FIR filter - Moving average filter (0) | 2023.04.09 |
| FIR filter - window 함수 그리고 실제로 구현가능한 Low pass filter (0) | 2023.04.09 |
| Convolution 수식을 보는 2가지 관점 (0) | 2023.04.03 |